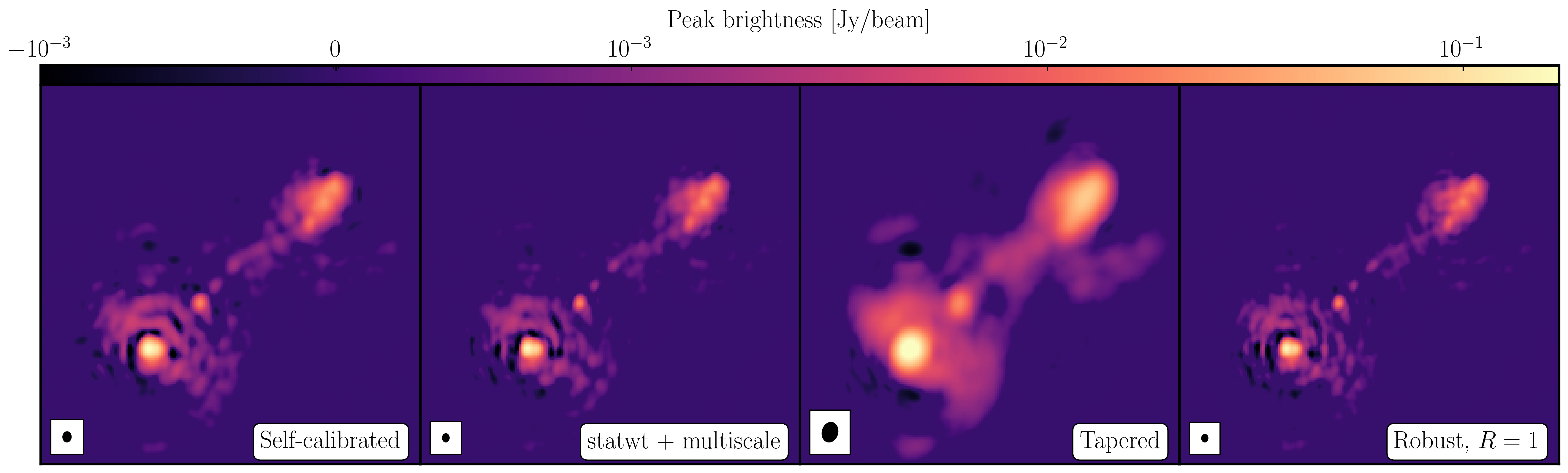
Advanced imaging
Data required
For this section, you want to download the fully self-calibrated data set which is contained in the tar bundle ERIS24_adv_imaging.tar.gz. This data-set has had the CORRECTED self-calibrated visibilities split into the DATA columns of this measurement set (to reduce the data size) and the most recent self-calibration model has been Fourier transformed into the measurement set (making a MODEL column).
You also want to copy the two calibration scripts that we have been using for the previous imaging and self-calibration tutorial. However, we have included copies of these scripts in the tar bundle. Ensure that you have the following in your folder,
1252+5634_adv_im.ms- fully self-calibrated visibilities3C277.1_imaging_outline2024.py- imaging script.3C277.1_imaging_all2024.py- cheat script containing the answers
Table of contents
1. Reweigh the data according to sensitivity (step 13)
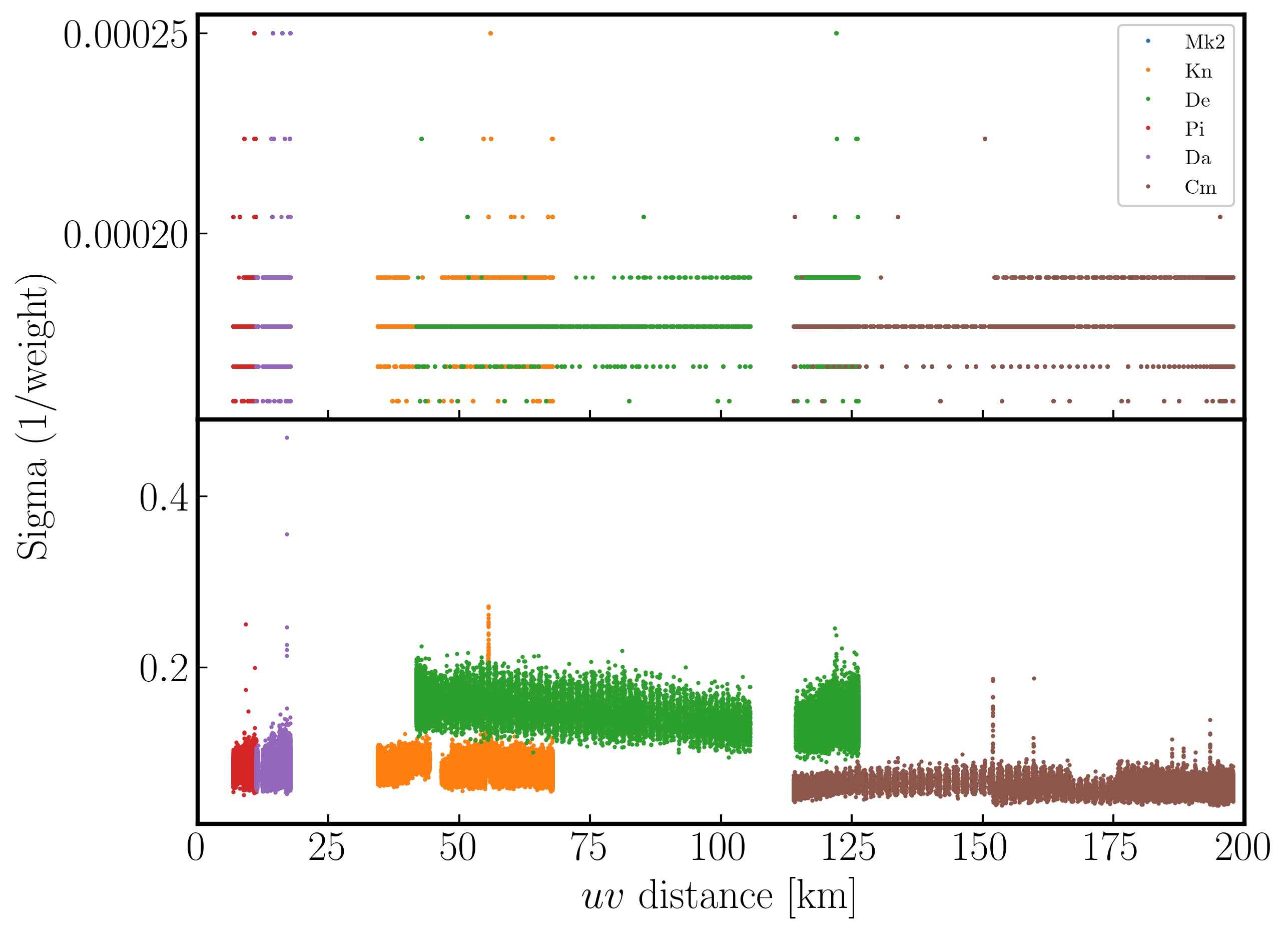
Often, especially for heterogeneous arrays, the assigned weighting is not optimal for sensitivity. For example, the Cambridge (Cm) telescope is more sensitive, therefore, to get the optimal image must be given a larger weight than the other arrays.
To recalculate the optimal weights we use the task statwt calculates the weights based on the scatter in small samples of data. Note that the original data are overwritten, so you might want to copy the MS to a different name or directory first.
There are alot of options here, but we are just going to use the default options. You can try with different weightings if you'd like.
- Take a look at step 13 and you will see three commands. The
plotmsstep will plot the weights before and after while thestatwtcommand will rescale the weights. Note that we are going to use the residual column to estimate the scatter (which is the data$-$model column)statwt(vis='**', datacolumn='residual_data') - Enter the relevant parameters (remembering we are using a different measurement set) and execute step 13
- Take a look at the
plotmsresults
In the plot below, we show the weights before (top panel) and after re-weighting (bottom panel) on the baselines to our refant (Mk2). As you can see, the telescopes have similar weights despite Cm being more sensitive. With the use of statwt, the weights now reflect the sensitivities, with Cm having the lowest sigma weight so is more sensitive.
2. Try multi-scale clean (step 14)
Let's image the re-weighted data using multiscale clean, which instead assumes that the sky can be represented by a bunch of Gaussians rather than delta functions.
- Look at step 14 and enter the imaging parameters for multi scale clean. Have a look at the help for the
tcleantask, which suggests suitable values of thescaleparameter.Linuxtclean(vis=target+'_adv_im.ms', imagename='advIMmulti', imsize=['**','**'], cell='**arcsec', specmode='mfs', niter=3000, cycleniter=300, gain=0.2, threshold=0, deconvolver='mtmfs', scales=['**','**','**'], nterms=2, interactive=True)Mac OSrun_iclean(vis=target+'_adv_im.ms', imagename='advIMmulti', imsize=['**','**'], cell='**arcsec', specmode='mfs', niter=3000, cycleniter=300, gain=0.2, threshold=0, deconvolver='mtmfs', scales=['**','**','**'], nterms=2)rmsmulti=imstat(imagename='advIMmulti.image.tt0', box='**,**,**,**')['rms'][0] peakmulti=imstat(imagename='advIMmulti.image.tt0', box='**,**,**,**')['max'][0] print('advIMmulti.image.tt0 rms = %7.3f mJy/bm' % (rmsmulti*1000.)) print('advIMmulti.image.tt0 peak = %7.3f mJy/bm' % (peakmulti*1000.)) print('advIMmulti.image.tt0 S/N = %7.3f' % (peakmulti/rmsmulti)) - Once you are happy, execute step 14 and deconvolve the image
You will find that the beam is now slightly smaller (I got $52\times42\,\mathrm{mas}$) as the longer baselines have more weight, so the peak is lower). I got $S_p \sim 149.235 \,\mathrm{mJy\,beam^{-1}}$ and $\sigma \sim 50\,\mathrm{\mu Jy\,beam^{-1}}$ when using a scales=[0,2,5]. Note that this gives a lower S/N despite the optimal reweighting. This is mainly because the beam area is smaller and hence the peak flux in beam area units is lower.
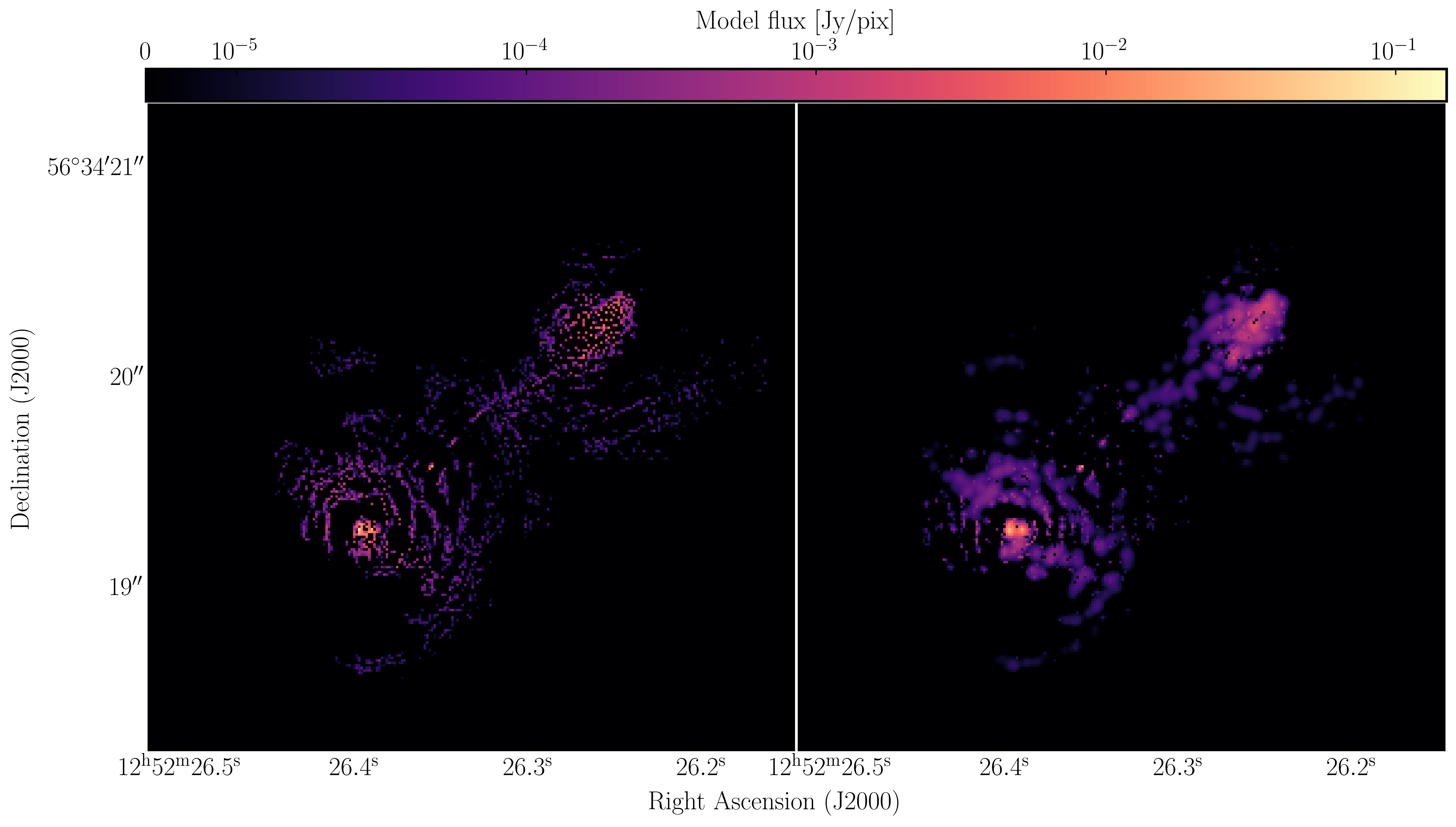
With multi-scale CLEAN we can look at the two models to see the difference between them. Often multi-scale is required when you are dominated by diffuse emission and can then be used to improve the self-calibration model. Below, I have plotted the models using just standard delta function CLEAN and the multi-scale clean.
3. Taper the visibilities during imaging (step 15)
Next we shall experiment with changing the relative weights given to longer baselines. Applying a taper reduces this, giving a larger synthesised beam more sensitive to extended emission. This just changes the weights during gridding for imaging, no permanent change to the uv data. However, strong tapering increases the noise.
- Look at the $uv$ distance plot and choose an outer taper (half-power of Gaussian taper applied to data) which is about 2/3 of the longest baseline. Units are wavelengths, so calculate that or plot amplitude vs. uvwave.
- Enter this and the imaging parameters into step 15 and execute,
Linux
tclean(vis=target+'_adv_im.ms', imagename='advIMtaper', imsize=['**','**'], cell='**arcsec', specmode='mfs', niter=4000, cycleniter=300, gain=0.2, threshold=0, deconvolver='mtmfs', uvtaper=['**Mlambda'], scales=[0], nterms=2, interactive=True)Mac OSrun_iclean(vis=target+'_adv_im.ms', imagename='advIMtaper', imsize=['**','**'], cell='**arcsec', uvrange='<**Mlambda', #uvtaper not supported specmode='mfs', niter=4000, cycleniter=300, gain=0.2, threshold=0, deconvolver='mtmfs', scales=[0], nterms=2)rmstaper=imstat(imagename='advIMtaper.image.tt0', box='**,**,**,**')['rms'][0] peaktaper=imstat(imagename='advIMtaper.image.tt0', box='**,**,**,**')['max'][0] - Inspect the image and check the beam size and the image statistics.
For a taper of 2.5 Mlambda I managed to get a restoring beam size of $129\times100\,\mathrm{mas}$, a peak brightness of $S_p \sim 265.595\,\mathrm{mJy\,beam^{-1}}$ and an rms noise of $\sigma \sim 78\,\mathrm{\mu Jy\,beam^{-1}}$.
4. Different imaging weights: Briggs robust (step 16)
In our final experimentation with imaging we shall change the relative weights given to longer baselines. Default natural weighting gives zero weight to parts of the $uv$ plane with no samples. Briggs weighting interpolates between samples, giving more weight to the interpolated areas for lower values of robust. For an array like e-MERLIN with sparser sampling on long baselines, this has the effect of increasing their contribution, i.e., making the synthesised beam smaller. This may bring up the jet/core in more detail, at the expense of the extended lobes. Low values of robust increase the noise. You can combine with tapering or multiscale, but initially remove these parameters.
- Take a look at step 16 and enter the parameters to conduct imaging with Briggs weighting and a robust value of 1. Remember to use the help function to find the correct inputs.
Linux
tclean(vis=target+'_adv_im.ms', imagename='advIMrobust', imsize=['**','**'], cell='**arcsec', specmode='mfs', niter=4000, cycleniter=300, gain=0.2, threshold=0, deconvolver='mtmfs', nterms=2, weighting='**', robust='**', interactive=True)Mac OSrun_iclean(vis=target+'_adv_im.ms', imagename='advIMrobust', imsize=['**','**'], cell='**arcsec', specmode='mfs', niter=4000, cycleniter=300, gain=0.2, threshold=0, deconvolver='mtmfs', nterms=2, weighting='**', robust='**')rmsrobust=imstat(imagename='advIMrobust.image.tt0', box='**,**,**,**')['rms'][0] peakrobust=imstat(imagename='advIMrobust.image.tt0', box='**,**,**,**')['max'][0] - Once you are done, execute and clean the image.
- If you have time, you can also experiment with other robust values and weighting schemes.
With a robust parameter of 1, I made an image with a restoring beam of $48\times39\,\mathrm{mas}$, $S_p \sim 143.404\,\mathrm{mJy\,beam^{-1}}$ and $\sigma \sim 52\,\mathrm{\mu Jy\,beam^{-1}}$
5. Summary and conclusions
This tutorial investigated the various imaging techniques which can be used to extenuate features. In the first instance we used statwt to optimally reweigh the data to have maximum sensitivity. We find that the Cm telescope is the most sensitive (as it is 32m wide), but also contains all the long baselines. As a result these long baselines are expressed more when imaging resulting in a higher resolution image than what we've seen before. As a result the peak flux reduces but so did the sensitivity! In addition, we used multiscale clean to better deconvolve the large fluffy structures which standard clean can struggle with.
The next step that we did was to taper the weights with respect to $uv$ distance. The downweighting of the long baselines means that we are more sensitive to larger structures hence our resolution is lower. However, because of the sensitivity contained in these long baselines, we have a much larger rms.
And finally, we introduced robust weighting schemes. These schemes provide a clear way to achieve intermediate resolutions between naturally weighted and uniformly weighted data.
| Peak brightness | Noise (rms) | S/N | Beam size | |
|---|---|---|---|---|
| [$\mathrm{mJy\,beam^{-1}}$] | [$\mathrm{mJy\,beam^{-1}}$] | [$\mathrm{mas\times mas}$] | ||
| statwt + multiscale | 148.235 | 0.050 | 2964.7 | 52 $\times$ 42 |
| Tapering | 265.595 | 0.078 | 3405.1 | 129 $\times$ 100 |
| Robust weighting ($R=1$) | 143.404 | 0.052 | 2757.8 | 48 $\times$ 39 |