Calibration

Data required

This tutorial continues from the same dataset, and set of python scripts that the first tutorial starts with. You should have at least the files in your current working directory,

  • all_avg.ms - the data (after conversion to a measurement set).
  • 3C286_C.clean.model.tt0 - used for fluxscaling of the data set.
  • all_avg_all.flags.txt - all flags
  • 0319+4130_flags.txt - empty flagging file for bandpass calibrator
  • 0319+4130_flags_answers.txt - complete flagging file for bandpass calibrator
  • 3C277.1_cal_outline2024.py - the script that we shall input values into to calibrate these data.
  • 3C277.1_cal_all2024.py - cheat script for calibating these data.

Important: before you begin this tutorial, we want to ensure that your data-sets are identical (to save time). Please enter the following two commands into a CASA prompt to ensure the flagging is identical

runsteps=[10]
execfile('3C277.1_cal_outline2024.py')

Table of contents

  1. Setting the flux of the primary flux scale calibrator (11)
  2. Bandpass calibration
    1. Decorrelation and solution intervals (12)
    2. Pre-bandpass calibration (13)
    3. Derive bandpass solutions (14)
  3. Time-dependent delay calibration (15)
    1. Inspect effects (16)
  4. Gain calibration (17)
    1. Time-dependent phase calibration of all calibration sources
    2. Time-dependent amplitude calibration of all calibration sources
  5. Determining true flux densities of other calibration sources (18-19)
  6. Apply solutions to target (20-21)

1. Setting the flux of the primary flux scale calibrator (step 11)

← back to top

The first thing that we are going to do is set the flux density of the flux scale calibrators (which is in this case 3C286 and 3C84). This is important as the correlator outputs the visibilities with a arbitrary scaling so it is not in physical units i.e., Janskys. However, the visibilities amplitudes are correct relative to each other. This means that we can observe a standard source with a physically known flux density (similar to the zero points of a temperature scale) which then can be used to rescale the visibilities and put all fields onto this scale.

In this observation, we observed 1331+3030 (= 3C286) is an almost non-variable radio galaxy and its total flux density is very well known as a function of time and frequency (Perley & Butler 2013). However, this flux density standard was derived through VLA observations and the source is somewhat resolved by e-MERLIN.

To mitigate this, we use a model made from a ~12 hr observation centred on 5.5 GHz. This is scaled to the current observing frequency range (around 5 GHz) using setjy which derives the appropriate total flux density, spectral index and curvature using parameters from Perley & Butler (2013).

However, a few percent of the flux is resolved-out by e-MERLIN; the simplest way (at present) to account for this is later to scale the fluxes derived for the other calibration sources by 0.938 (based on calculations for e-MERLIN by Fenech et al.).

The model is a set of delta functions and setjy enters these in the Measurement Set so that their Fourier Transform can be used as a $uv$-plane model to compare later with the actual visibility amplitudes. If you make a mistake (e.g. set a model for the wrong source) use task delmod to remove it.

  • Take a look at step 11. Enter the correct parameters for the setjy task and flux scaling of 3C286. 
    	setjy(vis='**',
		  field='**', reffreq='5.073e9Hz',
		  standard='Perley-Butler 2013', spix=-0.66,
		  model='**', usescratch=True) # You should have downloaded and decompressed this model
  • Have a look at the other commands in step 11 which are completed for you. By default, setjy scales the model for each channel, as seen if you plot the model amplitudes against $uv$ distance, coloured by spectral window. The first plotms command (shown below) will plot the model versus $uv$ distance. The model only appears for the baselines present for the short time interval for which 1331+3030 was observed here. 
    	plotms(vis='all_avg.ms', field='1331+3030', xaxis='uvwave',
		   yaxis='amp', coloraxis='spw',ydatacolumn='model',
		   correlation='LL,RR',symbolsize=4, 
		   showgui=gui,overwrite=True,   
		   plotfile='3C286_model.png')

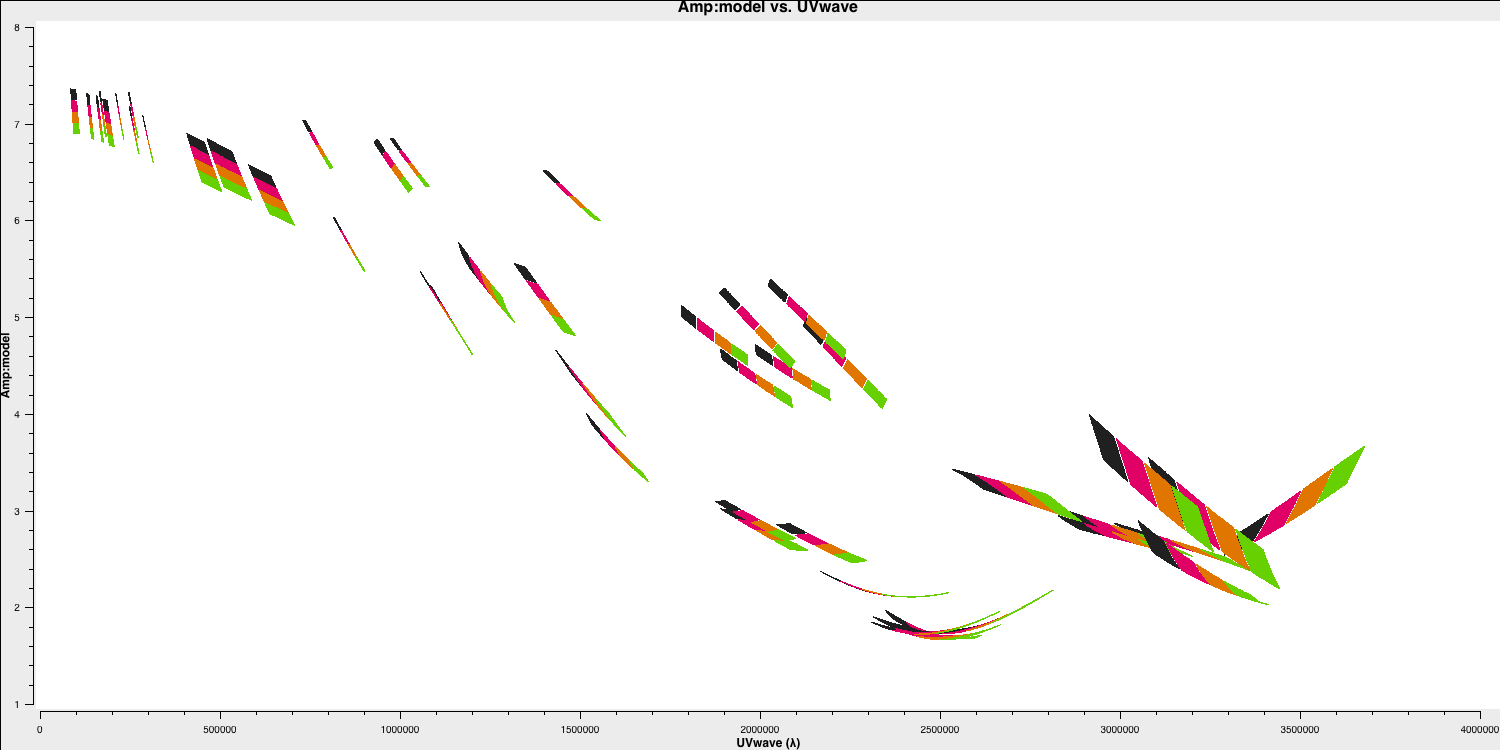
  • While this is not normal for e-MERLIN data, we are also setting the flux density of the bandpass calibrator (0319+4130) in this step. Normally, we would derive it's flux density from 3C286 and then derive the bandpass calibration twice (once without taking into account spectral indices and then taking it into account). 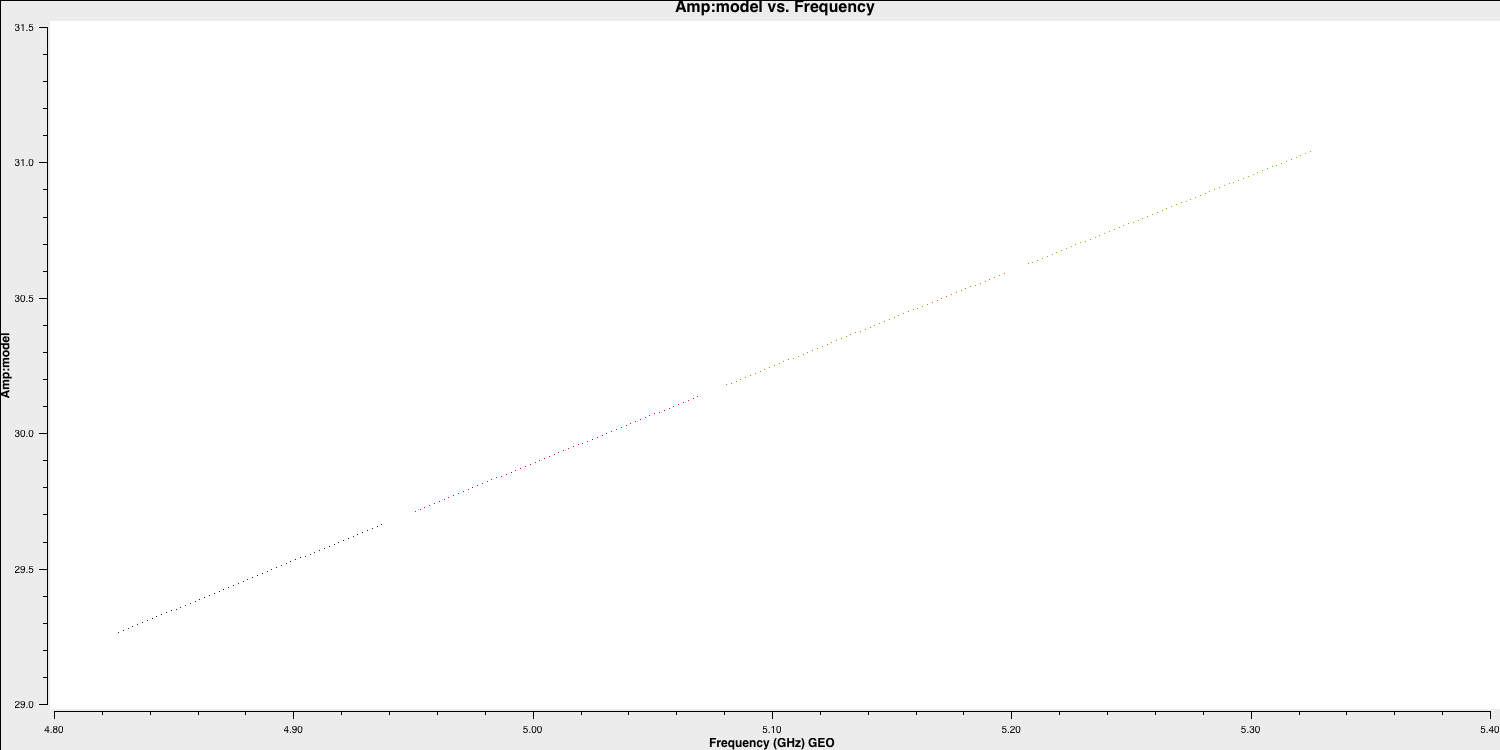This source is pretty well known so, to save extra calibration steps, we are going to set its flux density here and the spectral index, spix, with the following code (done for you).
    	setjy(vis='all_avg.ms',
	      field='0319+4130',
	      standard='manual',
	      fluxdensity=[30.1388, 0.0, 0.0, 0.0],
	      spix = 0.6, reffreq= '5.07GHz')
  • This source is not resolved by e-MERLIN therefore the model that we are going to use is that of a point source. Hence, the following plotms step should have a slope of 0.6 in amplitude versus frequency with a flux density of $30.1388\,\mathrm{Jy}$ at $5.07\,\mathrm{GHz}$
    	plotms(vis='all_avg.ms', field='0319+4130', xaxis='freq',
		   yaxis='amp', coloraxis='spw',ydatacolumn='model',
		   correlation='LL,RR',symbolsize=4, 
		   showgui=gui,overwrite=True,   
		   plotfile='3C84_model.png')

2. Bandpass calibration

2A. Investigating decorrelation and solution intervals (step 12)

← back to top

We have set the primary fluxes of the main flux / bandpass calibrators and now we can move onto calibrating for the instrumental/atmospheric effects. If you remember from your interferometry introduction, we have used a model of the locations of our telescopes which corrects for the geometric delay and ensures that our signal from the source interferes constructively between all antennae. However, the atmosphere, electronics/engineering of the antennae, and clock/timing errors changes the phase and prevents perfect constructive interference. We therefore have to correct for this.

To correct for this, our standard calibration assumes that your calibrator sources are point-like (i.e., flat in amplitude and zero in phase). This means that any deviation must be due to an error. Secondly, there is an assumption that the errors are antenna independent i.e., there must be a common factor/error on each baseline to the same antenna. This is sensible as each antenna will have different clocks (in the case of VLBI), different atmospheric line-of-sights, different LNAs etc etc. This also means that we should be able to derive a per antenna solution and prevents us from simply making our visibilities looking like a point source (if we solved per baseline).

We are going to calibrate the bandpass calibrator (0319+4130) first with the goal of generating a bandpass calibration table. The bandpass is the response of the antenna (both amplitude and phase) against frequency. This changes quickly with frequency, but is not expected to change against time (at least during the observation) as it is typically due to filters and receiver sensitivities within the antenna. This means we need to get solutions on each channel so we need a very bright source (0319 is 20-30 Jy so very bright) in order to get enough signal on each small bandwidth of the channel. However, before we can derive this correction, we need to first calibrate the other sources of error affecting this source first in order to isolate the bandpass correction.

To begin, we are going to correct for the phase errors, $\Delta\Theta$, which can primarily be parameterised by a constant plus higher order terms: $$\Delta\Theta = \Theta(t,\nu) + \frac{\partial \Theta}{\partial \nu} + \frac{\partial \Theta}{\partial t}$$ We call $\Theta(t,\nu)$ the phase error, the slope in frequency space, $\frac{\partial \Theta}{\partial \nu}$, the delay error and the slope against time, $\frac{\partial \Theta}{\partial t}$, the rate error. The rate error and higher order terms are only typically needed for long baseline or low frequencies where more turbulent atmospheric conditions and separate clocks cause errors. Most modern interferometers including e-MERLIN often only need to consider the delay and phase terms.

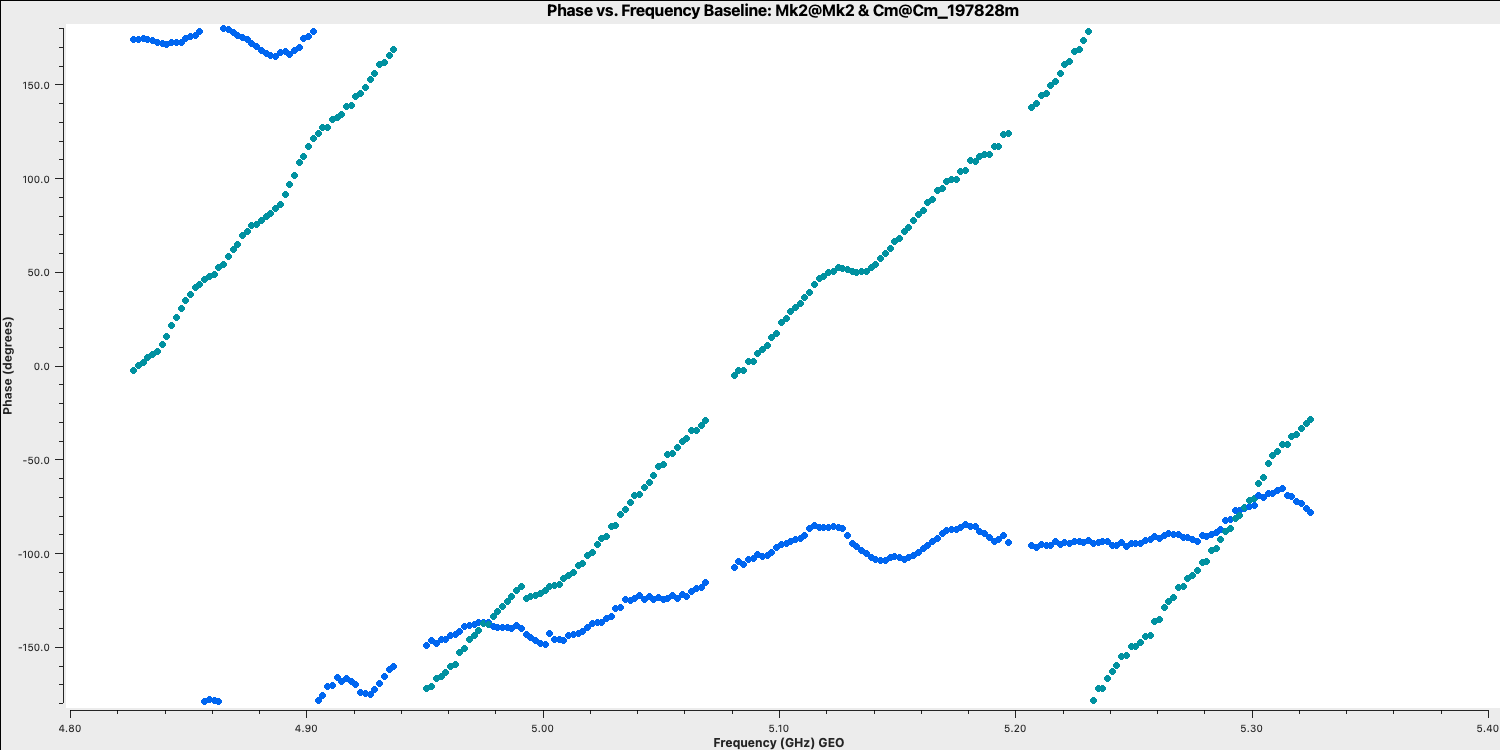
  • Take a look at step 12. It is advised for this step to copy the individual plotms commands directly into CASA!
  • Copy the first command into CASA which will plot the phase versus time for a bright source i.e., our bandpass calibrator (so we can see the visibilities above the noise). Note that we are selecting just one scan of this source. 
    	plotms(vis='all_avg.ms', field='0319+4130', 
	       xaxis='frequency',yaxis='phase',
	       gridrows=5,gridcols=1,iteraxis='baseline',
	       xselfscale=True,xsharedaxis=True,
	       ydatacolumn='data',antenna=antref+'&*',
	       avgtime='2400',correlation='LL,RR',
	       coloraxis='corr', scan='92',
	       plotfile='',plotrange=[-1,-1,-180,180],
	       showgui=gui,                    # change to True to inspect by interval or antenna
	       overwrite=True)

The y-axis spans $-180$ to $+180$ deg and some data has a slope of about a full 360 deg across the 512 MHz bandwidth. Looking at the baseline the Cambridge, think about the following questions.

QUESTION 1: What is the apparent delay error this corresponds to? What will be the effect on the amplitudes?

Click for answerA change of $2\pi$ radians in $x$ Hz results from a delay error of $1/x$ sec. So a change of 360 deg in 512 MHz is produced by a delay error of $1/(512\times 10^{6})\,\mathrm{sec} \sim 2\,\mathrm{ns}$. If data are vector-averaged across a phase slope, the amplitudes will be reduced, by a larger amount the greater the phase change in the averaging interval, so if the combined phase change on a baseline is worse in one polarisation than the other, that polarization will have a lower averaged apparent amplitude.

QUESTION 2: Delay corrections are calculated relative to a reference antenna which has its phase assumed to be zero, so the corrections factorised per other antenna include any correction due to the refant. Roughly what do you expect the magnitude of the Cm corrections to be? Do you expect the two hands of polarisation to have the same sign?

Click for answer The slopes on Mk2 correspond to about 1 turn in 512 MHz, in the same sense for both LL and RR. The slopes on Cm correspond to less than half a turn in the same sense for one polarisation, and about a full turn in the opposite sense for the other. So the combination of errors, which will be solved entirely by correcting Cm, corresponds to magnitudes of $\lesssim 1\,\mathrm{ns}$ and $\sim 4\,\mathrm{ns}$ for the two polarisations, with opposite signs. The slopes, and hence the actual values, vary between spw, see the delay correction plot.

  • Have a look at the second and third plotms commands which shows what happens if we average these data without correcting for the delay slope. The first command plots the amplitude of one channel and one correlation on the longest baseline.
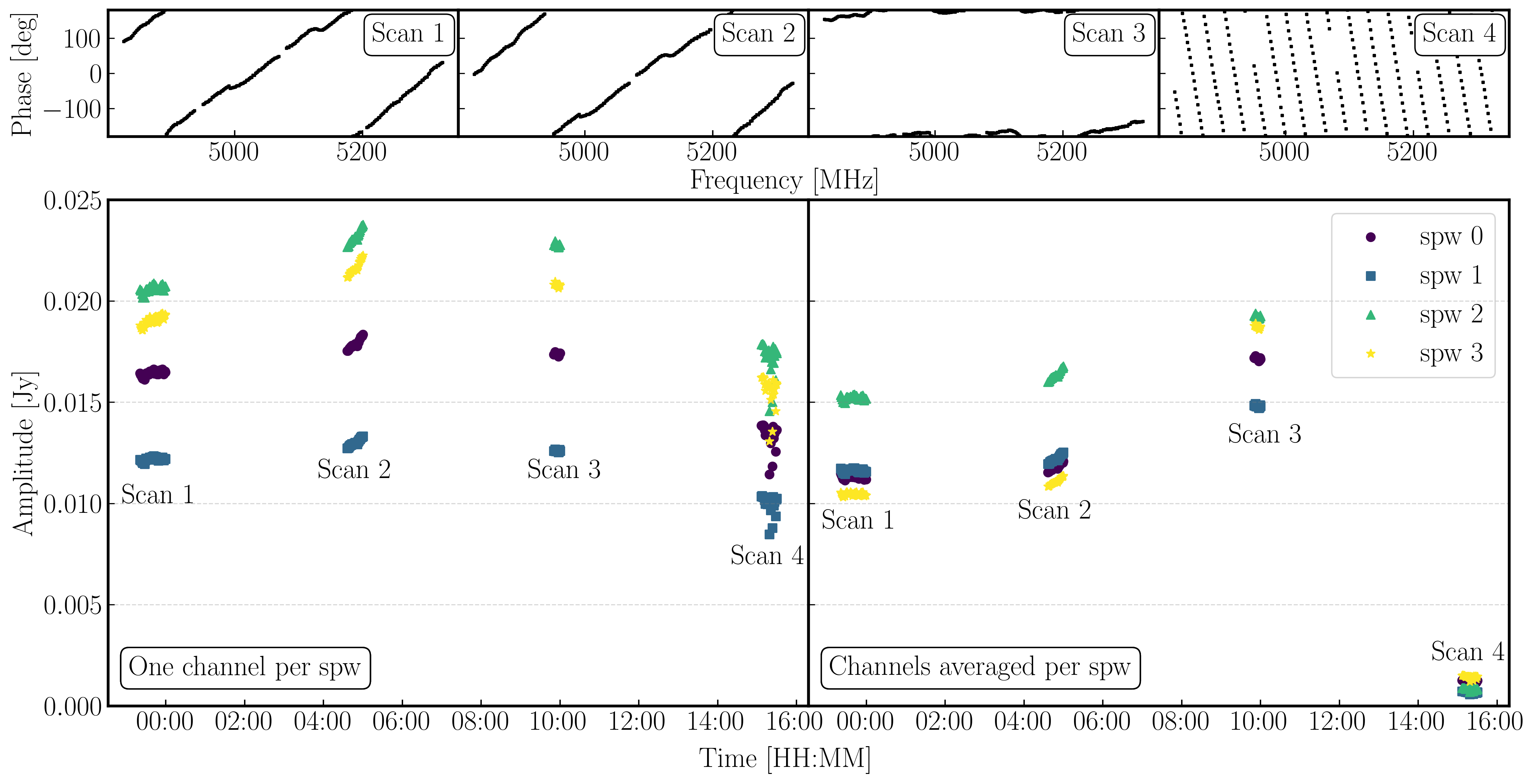
    	plotms(vis='all_avg.ms', field='0319+4130',
		   spw='0~3:55', ydatacolumn='data',                     # Just one channel per spw
		   yaxis='amp', xaxis='time', plotrange=[-1,-1,0,0.025], # Plot amplitude v. time with fixed y scale
		   avgtime='60',correlation='RR', antenna=antref+'&Cm',  # 60-sec average, one baseline/pol
		   coloraxis='spw',plotfile='',
		   showgui=gui,
		   overwrite=True)
    The next command plots the same but now we are averaging the channels together, 
     	plotms(vis='all_avg.ms', field='0319+4130',
		   xaxis='time', yaxis='amp',ydatacolumn='data',
		   spw='0~3',avgchannel='64',
		   antenna=antref+'&Cm', avgtime='60',correlation='RR',
		   plotrange=[-1,-1,0,0.025],coloraxis='spw',
		   plotfile='',
		   showgui=gui,                    # change to T to inspect closely
		   overwrite=True)
  • QUESTION 3: Take a look at the two plots and compare. Which has the higher amplitudes - the channel-averaged data or the single channel? Why?
    Click for answerThe single channel has the higher amplitudes. The source 3C84 is very bright so there is plenty of signal in each single channel. But averaging over all channels when there is a large phase slope causes the amplitudes to decorrelate so the channel-averaged data has depressed amplitudes. A similar effect is seen if you have data with phase errors as a function of time and average over too long a time period.

We have plotted the same amplitude versus time plots below in python for the four scans of the bandpass calibrator. As you can see, the effects of decorrelation of the amplitudes is more extreme when the delay error is larger (e.g., in scan 4)

Finally, in preparation for the calibration of the bandpass source, we want to derive the time-dependent phase solution interval. A solution interval is just the amount of time you average together to try and derive a correction. The selection of a solution interval can be tricky but it is all about timescales. On an integration to integration basis (few seconds), your visibilities will be dominated by thermal noise while on longer timescales, the general trends will be dominated by the instrumental / line-of-sight effects that we want to calibrate out. We therefore want to average enough data to track these effects and derive corrections but not over-average that we do not pick up on the detailed trends. We shall show this next

  • Take a look at the final plotms command in step 12,
    	plotms(vis='all_avg.ms',
		   field='0319+4130',
		   spw='0~3:55', correlation='RR',
		   antenna=antref+'&Cm',scan='1',
		   xaxis='time', yaxis='phase',ydatacolumn='data',
		   coloraxis='spw',plotfile='',
		   showgui=gui, overwrite=True)
  • We are just plotting the phase versus time of a single scan, single correlation and single channel of the bandpass calibrator. You should see a plot like that below (colorised by spw)

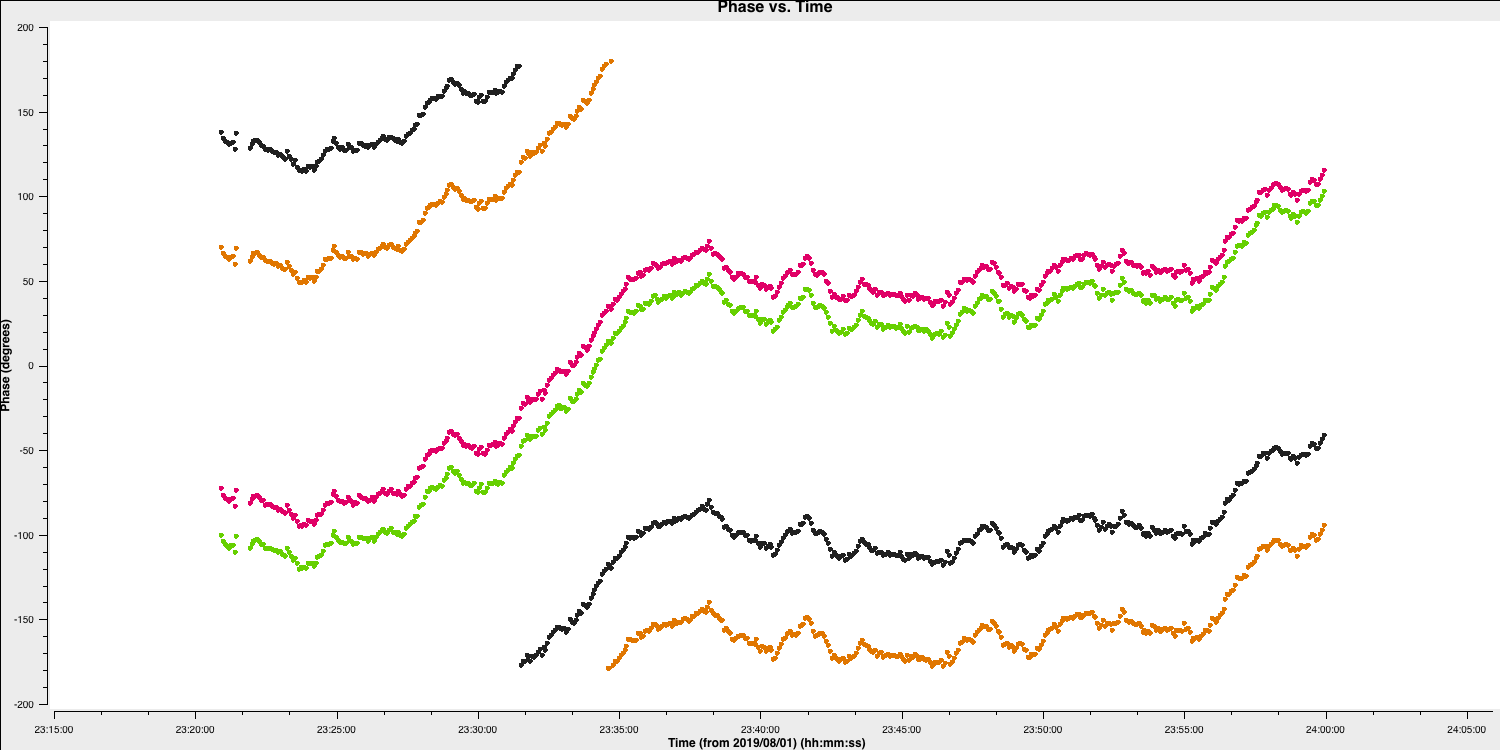
Some things to note here:

  1. On the 20-30s timescales we have trackable phase fluctutations caused by the atmosphere which causes the phases to drift.
  2. These fluctuations are similar across each spw indicating that the atmosphere affects our frequency range equally (meaning that we could fix the delay and combine spw for higher S/N solutions
  3. The delays are causing the absolute phase offsets between the spectral windows, but, crucially, these seem to not change with time (otherwise the gap between the spectral windows would change with time). Because of this, it is suitable to select a long solution interval (e.g., 600s in this case) for the delay calibration to maximise the S/N of our solutions.

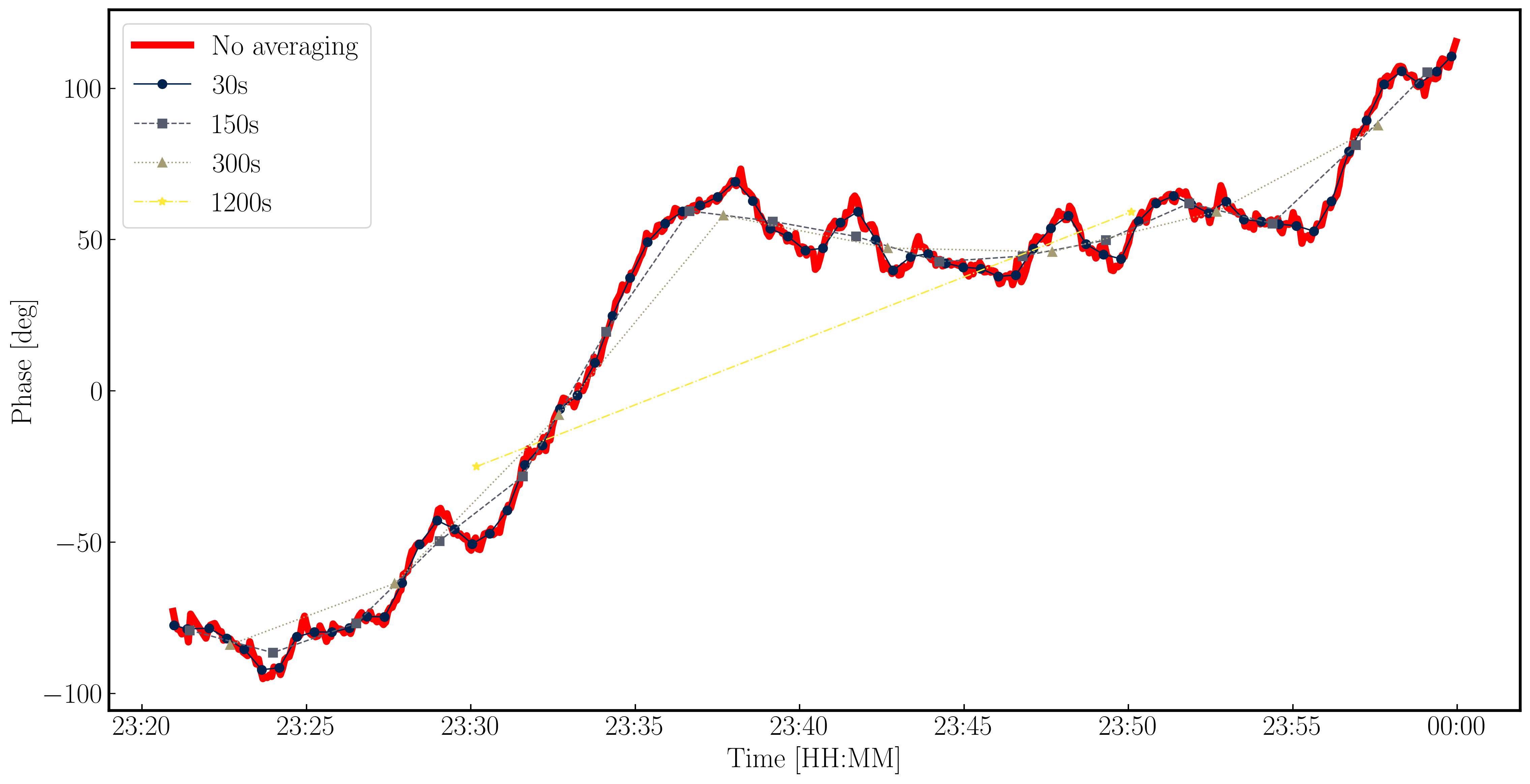
While we have decided on a solution interval for delays, we need to do the same for the phase term. In the plot below, we have overplotted the phase with different averaging intervals of just one spectral window. You can see that we start being unable to trace the general trends causes by the atmosphere when the averaging is too severe. Howevever, we can also see that there's negligible thermal noise on a intergration to integration basis, so we could actually use a very short solution interval such as the 30s shown in the plot. This would track the atmospheric fluctuations well.

2B. Pre-bandpass calibration (step 13)

With our solution intervals in hand, we are going to now conduct the gain calibration for us to isolate the bandpass corrections. This will allow us to calibrate out the atmosphere, clock errors etc etc. which changes our amplitudes and phases over time.

  • Again, for this step, it is advisable to copy and paste your tasks directly into CASA to do each calibration step bit by bit. If you are having syntax errors, remember that the variables gui = True and antref = 'Mk2' should have been set in CASA.
  • Have a look at step 13. We shall begin by calibrating the delays by using the CASA task gaincal. We saw from the figure in the previous section that the absolute offset between the phases of different spws remained almost the same hence the delay calibration did not change too much (hence can use a long solution interval). Fill in the missing code to generate the delay solutions for the bandpass calibrator. Remember to use help(gaincal)!
    	gaincal(vis='all_avg.ms',
			gaintype='**',
			field='**',
			caltable='bpcal.K',
			spw='0~3',solint='**',
			refant=antref,
			refantmode='strict',
			minblperant=2,
			minsnr=2)

The gaincal task will generate a calibration table (name bpcal.K in this case) which will include the delay solutions that, when applied to the visiblities, will remove that phase slope versus frequency we saw earlier. However, we always want to plot the solutions to ensure that they are decent. Good solutions are normally smoothly varying without jumps.

  • Take a look at the next plotms command and enter it into CASA
    	plotms(vis='bpcal.K',
	       xaxis='time',
	       yaxis='delay',
	       gridrows=3,gridcols=2,
	       iteraxis='antenna', coloraxis='spw',
	       xselfscale=True,
	       yselfscale=True,
	       plotfile='',
	       showgui=gui, overwrite=True)

This should produce a plot like that shown below.

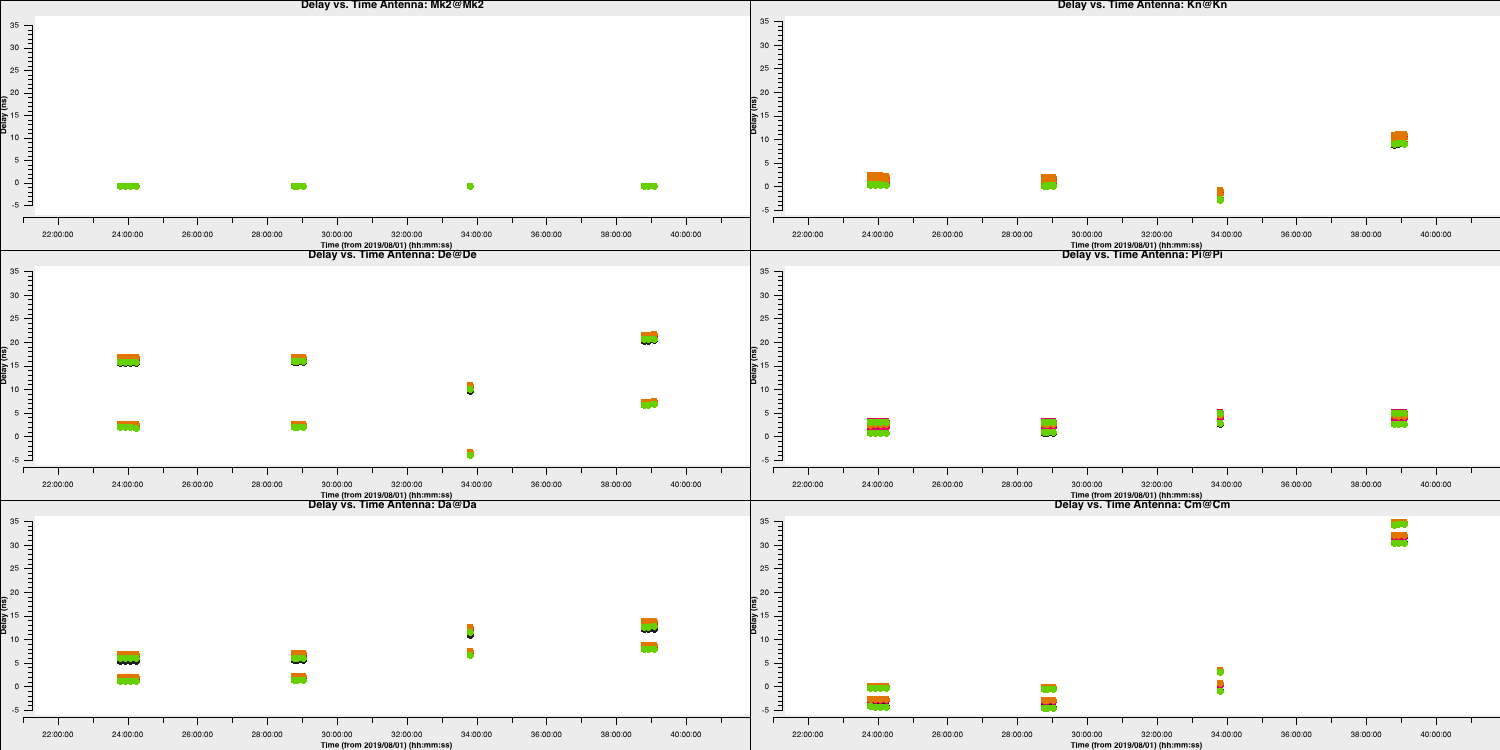
As you can see, the solutions are smooth and generally follow each other. Note the large delay correction for the Cm telescope in the last scan. We saw this in Section 4A where we plotted the amplitude decorrelation via averaging the channels. The huge delay (shown by the phase wrapping quickly), corresponds to the 35ns solutions for this scan on this telescope.

With the delay calibration for 0319+4130 complete, the offsets between the spectral windows in the frequency space would be removed and now we can concentrate on the time-dependent phase calibration which will remove the effect of the atmosphere along our line-of-sight to the source.

  • Take a look at the second gaincal command and enter in the parameters to perform a phase only calibration of the bandpass calibrator. Note that we include the delay calibration table in the gaintable parameter. CASA conducts calibration on the fly hence the delay table will be applied to the visibilities before the phase calibration is solved for.
    	gaincal(vis='all_avg.ms',
			calmode='**',
			field='**',
			caltable='bpcal_precal.p1',
			solint='**',
			refant=antref,
			refantmode='strict',
			minblperant=2,
			gaintable=['bpcal.K'],
			minsnr=2)
  • Again we want to plot the solutions to ensure that they are not just noise. 
    	plotms(vis='bpcal_precal.p1',
	       xaxis='time',
	       yaxis='phase',
	       gridrows=3,gridcols=2,
	       iteraxis='antenna', coloraxis='spw',
	       xselfscale=True,
	       yselfscale=True,
	       plotfile='',
	       showgui=gui, overwrite=True)

These solutions look great (I used a 30s interval`) and seem to follow the phases (and fluctuation timescales) we had seen before. Finally, we have one calibration step missing. We've done delays and phases and it's just amplitudes that are left!

  • Look at the final gaincal command and enter the correct parameters for amplitude only calibration of the calibrator. You will need to enter the gaintable parameter in this time. Note that we did not talk about the amplitude solution interval but typically these change slower than phases but need a higher S/N for good solutions (see 'closure amplitudes'). In this case, we will use 120s.
    	gaincal(vis='all_avg.ms',
			calmode='**',
			field='**',
			caltable='bpcal_precal.a1',
			solint='120s',
			solnorm=False,
			refant=antref,
			refantmode='strict',
			minblperant=2,
			gaintable=['**','**'],
			minsnr=2)
  • Finally, we want to plot these solutions to ensure they look ok and not noisy.
    	plotms(vis='bpcal_precal.a1',
	       xaxis='time',
	       yaxis='amp',
	       gridrows=3,gridcols=2,
	       iteraxis='antenna', coloraxis='spw',
	       xselfscale=True,
	       yselfscale=True,
	       plotfile='',
	       showgui=gui, overwrite=True)

These solutions look good. Note that the amplitudes are very low and that is to rescale the visibilities to the flux density that we had set right at the start of this section. We will do the same later for the other sources which we don't know the true flux densities of.

2C. Derive bandpass solutions (step 14)

With all other corruptions now having solutions through the three calibration tables we have derived. The final step is to derive the bandpass calibration table using a special task called bandpass.

  • Take a look at step 14, enter the correct parameters for the bandpass calibration and then enter this into the CASA prompt.
    	bandpass(vis='all_avg.ms',
			 caltable='bpcal.B1',
			 field='**',
			 fillgaps=16,
			 solint='inf',combine='scan',
			 solnorm='**',
			 refant=antref,
			 bandtype='B',
			 minblperant=2,
			 gaintable=['**','**','**'],
			 minsnr=3)

You may find a few complaints about failed solutions but these should be for the end channels that are flagged anyways.

  • Inspect the solutions using the plotms commands at the end of step 14
    	plotms(vis='bpcal.B1',
	       xaxis='freq',
	       yaxis='amp',
	       gridrows=3,gridcols=2,
	       iteraxis='antenna', coloraxis='corr',
	       xselfscale=True,
	       yselfscale=True,
	       plotfile='',
	       showgui=gui, overwrite=True)
    for amplitude and, 
    	plotms(vis='bpcal.B1',
	       xaxis='freq',
	       yaxis='phase',
	       gridrows=3,gridcols=2,
	       iteraxis='antenna', coloraxis='corr',
	       xselfscale=True,
	       yselfscale=True,
	       plotfile='',
	       showgui=gui, overwrite=True)
    for phase.

These should produce plots like those below which will correct for the receiver response on each antenna (note the close comparison to the plots when we flagged the edge channels). This error is antenna-based and direction-independent and so we can use it for all other sources as it should not change with time. Note that the spectral index of this source is taken into account here as it was specified in step 3A (normally you'd do the bandpass calibration twice with the second time using an estimate of the spectral index).

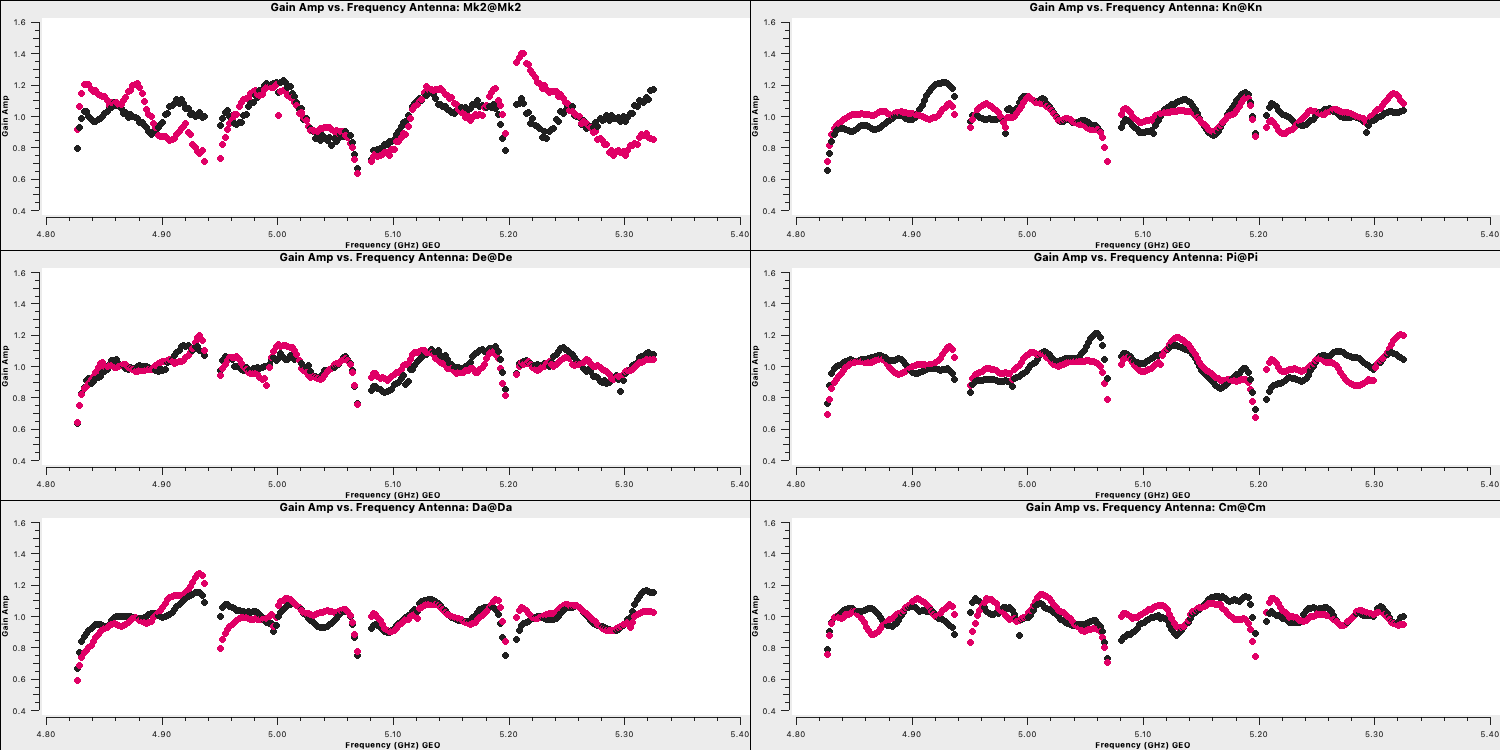
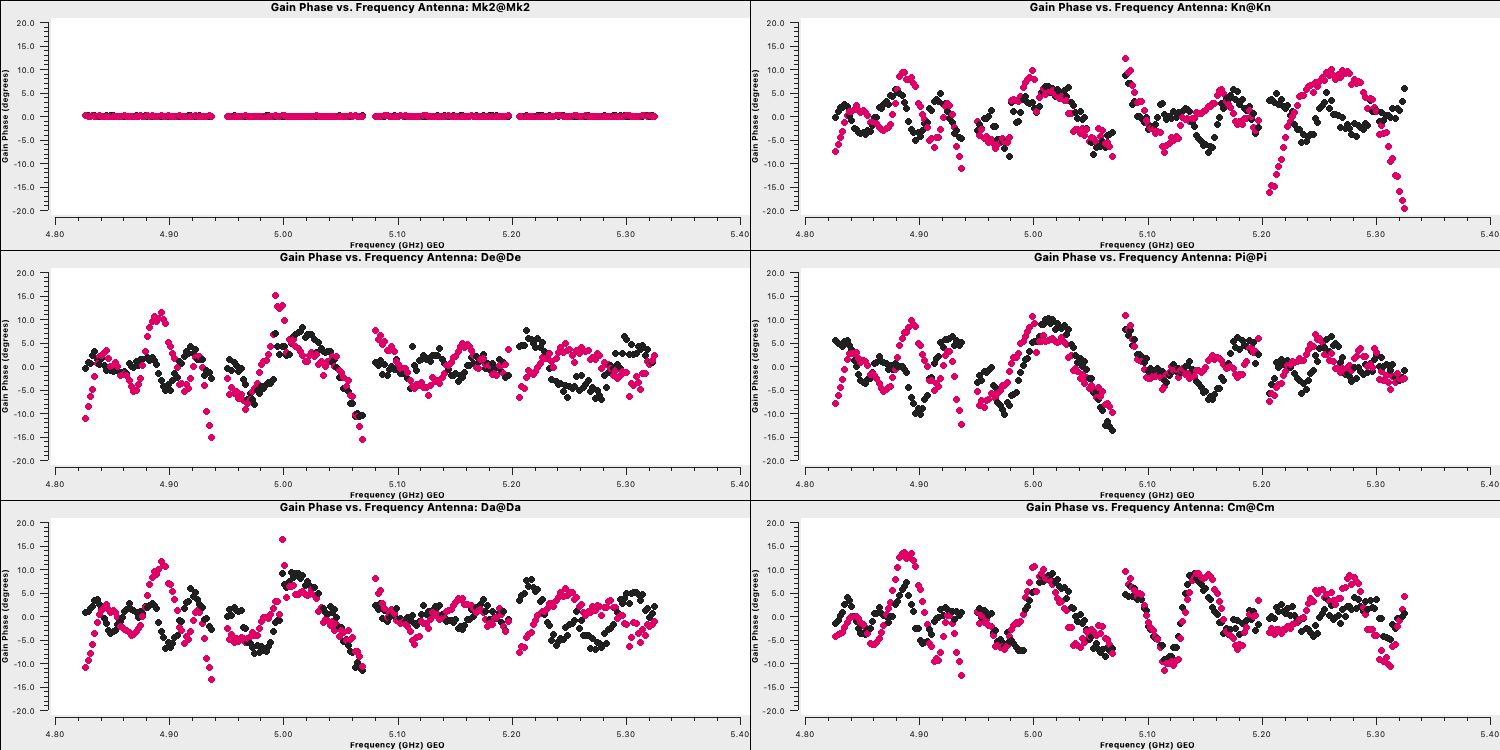
3. Time-dependent delay calibration (15)

← back to top

We've calibrated the bandpass calibrator in order to obtain the bandpass corrections. We now need to derive the time-dependent phase and amplitude corrections for all of the calibrators at once. This will allow us to perform phase referencing (remember this from the lecture) so we can observe the target source. Same as before, we will start with the delays and then will move onto the phase and amplitude corrections.

  • Take a look at step 15 and enter the parameters for both the gaincal command and the plotting command so that we can do delay calibration for all calibrator sources. The solution interval we used for the bandpass calibrator should be applicable here too. Remember that the bandpass calibration table should also be applied now!
    	gaincal(vis='all_avg.ms',
			gaintype='K',
			field='**',
			caltable='all_avg.K',
			spw='0~3',solint='**',
			refant=antref,
			refantmode='strict',
			gaintable=['**'], 
			minblperant=2,
			minsnr=2)

	plotms(vis='all_avg.K',
	       xaxis='**',
	       yaxis='**',
	       gridrows=3,gridcols=2,
	       iteraxis='antenna', coloraxis='spw',
	       xselfscale=True,
	       yselfscale=True,
	       plotfile='',
	       showgui=gui, overwrite=True)
  • Once you are happy execute step 15 and look at the output of plotms

You should end up with a plot that looks like this below. The solutions are smoothly varying with only a few jumps which shows that our solutions are ok.

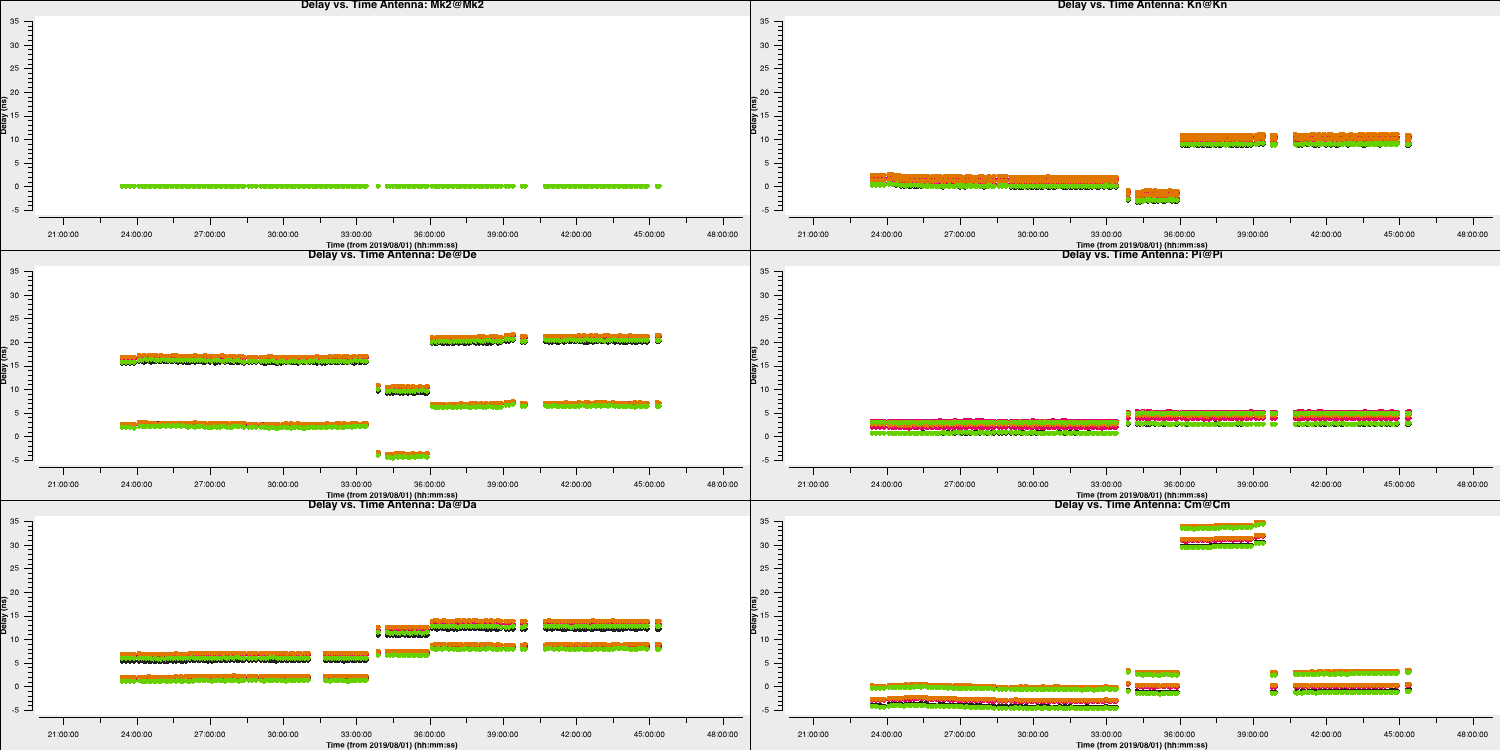
3A. Inspect effects of calibration (16)

Important: if you are short on time, skip this step and just read the information and plots shown here

In this step, we shall apply the delay and bandpass solutions to the calibration sources as a test, to check that they have the desired effect of producing a flat bandpass for the phase-reference source (not on the fly this time!). There is no need to apply the time-dependent calibration as we have not derived this for the phase-reference source yet anyway.

To apply these we shall use a task called applycal. Some notes about applycal:

  1. The first time applycal is run, it creates a CORRECTED data column in the MS, which is quite slow.
  2. Each time applycal is run, it replaces the entries in the CORRECTED column, i.e. the corrected column is not cumulative, but you can give applycal a cumulative list of gain tables.
  3. applymode can be used to flag data with failed solutions but we do not want that here as this is just a test.
  4. The interp parameter can take two values for each gaintable to be applied, the first determining interpolation in time and the second in frequency. The times of data to be corrected may coincide with, or be bracketed by the times of calibration solutions, in which case linear interpolation can be used, the default, normally used if applying solutions derived from a source to itself, or from phase ref to target in alternating scans. However, if solutions are to be extrapolated in time from one source to another which are not interleaved, then nearest is used. A similar argument covers frequency. There are additional modes not used here (see help(applycal)).
The delay correction ('K') table contains entries for all sources except the target. so we can use linear interpolation for this one. The bandpass table only has one entry so we cannot interpolate hence we'd want to select the nearest solutions.

  • Fill in the applycal step in step 16 and look at the following plotms command which will plot the 'before and after' phase reference phase and amplitude against frequency.
    	applycal(vis='all_avg.ms',
			 field='1302+5748,0319+4130,1331+3030',
			 calwt=False,
			 applymode='calonly',
			 gaintable=['**','**'],
			 interp=['**','**,**'])
  • Execute step 16 and take a look at the plots saved to the current directory.

The plot below shows the uncorrected and corrected amplitudes and phases for the Mk2-Cm baseline of the phase reference source (1302+5748) that is coloured by scan. It has been replotted in python for clarity!

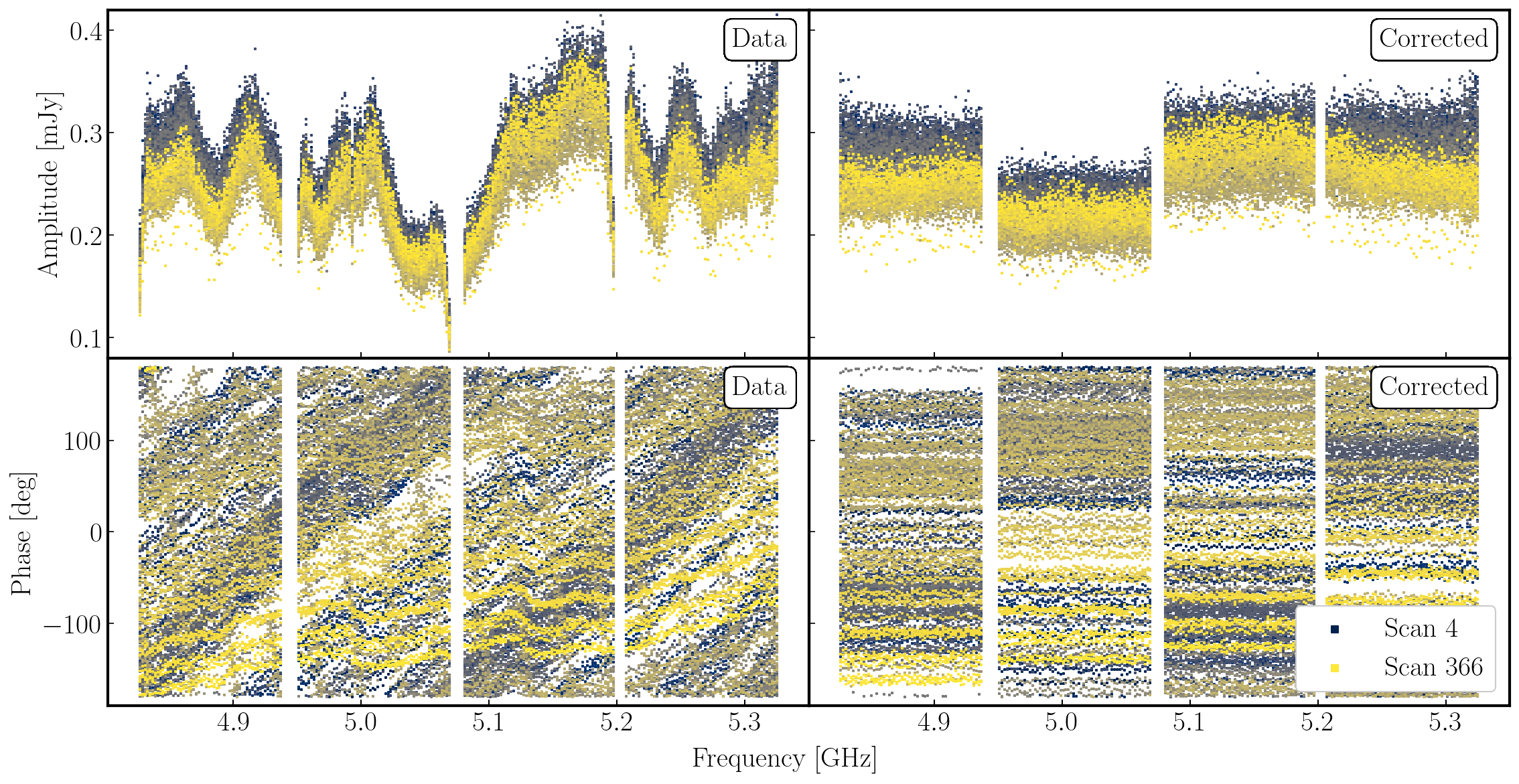
In the figure, each scan is coloured separately and shows a random offset in phase and some discrepancies in amplitude compared to other scans, but for each individual time interval it is quite flat. So we can average in frequency across each spw and plot the data to show remaining, time-dependent errors.

4. Gain calibration (step 17)

4A. Time dependent phase calibration

← back to top

As with the bandpass calibrator, we now move onto correcting for the phase fluctuations caused by tubulence in the atmosphere. This will allow us to phase reference and see our target source as the phase calibrator is approximately along the same line-of-sight.

  • Take a look at step 17 and insert the parameters that will allow us to conduct time-dependent phase calibration of all calibrator sources
    	gaincal(vis='all_avg.ms',
			calmode='p',
			caltable='calsources.p1',
			field='**,**,**',
			solint='**',
			refant=antref,
			refantmode='strict',
			minblperant=2,minsnr=1,
			gaintable=['all_avg.K','bpcal.B1'],
			interp=['linear','nearest,nearest'])
  • Copy this into the CASA propmt and run to generate the calibration table and have a look at the logger

The logger should show something like (if you used 16s solution intervals like me):

2022-08-12 10:08:20	INFO		Writing solutions to table: calsources.p1
2022-08-12 10:08:21	INFO	calibrater::solve	Finished solving.
2022-08-12 10:08:21	INFO	gaincal::::casa	Calibration solve statistics per spw:  (expected/attempted/succeeded):
2022-08-12 10:08:22	INFO	gaincal::::casa	  Spw 0: 1988/1572/1571
2022-08-12 10:08:22	INFO	gaincal::::casa	  Spw 1: 1988/1572/1571
2022-08-12 10:08:22	INFO	gaincal::::casa	  Spw 2: 1988/1572/1571
2022-08-12 10:08:22	INFO	gaincal::::casa	  Spw 3: 1988/1572/1571

This means that although there are 1988 16s intervals one the calibration sources data, about a fifth (1988−1572=416) of them have been partly or totally flagged. But almost all (99.93%) of the intervals which do have enough unflagged ('attempted') data gave good solutions ('succeeded'). There are no further messages about completely flagged data but in the terminal you see a few messages when there are fewer than the requested 2 baselines per antenna unflagged:

Found no unflagged data at:   (time=2019/08/02/21:00:04.5 field=0 spw=3 chan=0)
 Insufficient unflagged antennas to proceed with this solve.
   (time=2019/08/02/21:17:19.2 field=0 spw=3 chan=0)

Here, there are very few predicable failures. If there were many or unexpected failures, investigate - perhaps there are unflagged bad data, or pre-calibration has not been applied, or an inappropriate solution interval was used.

  • Plot the solutions and you should get something which tracks the phases well (as seen below)

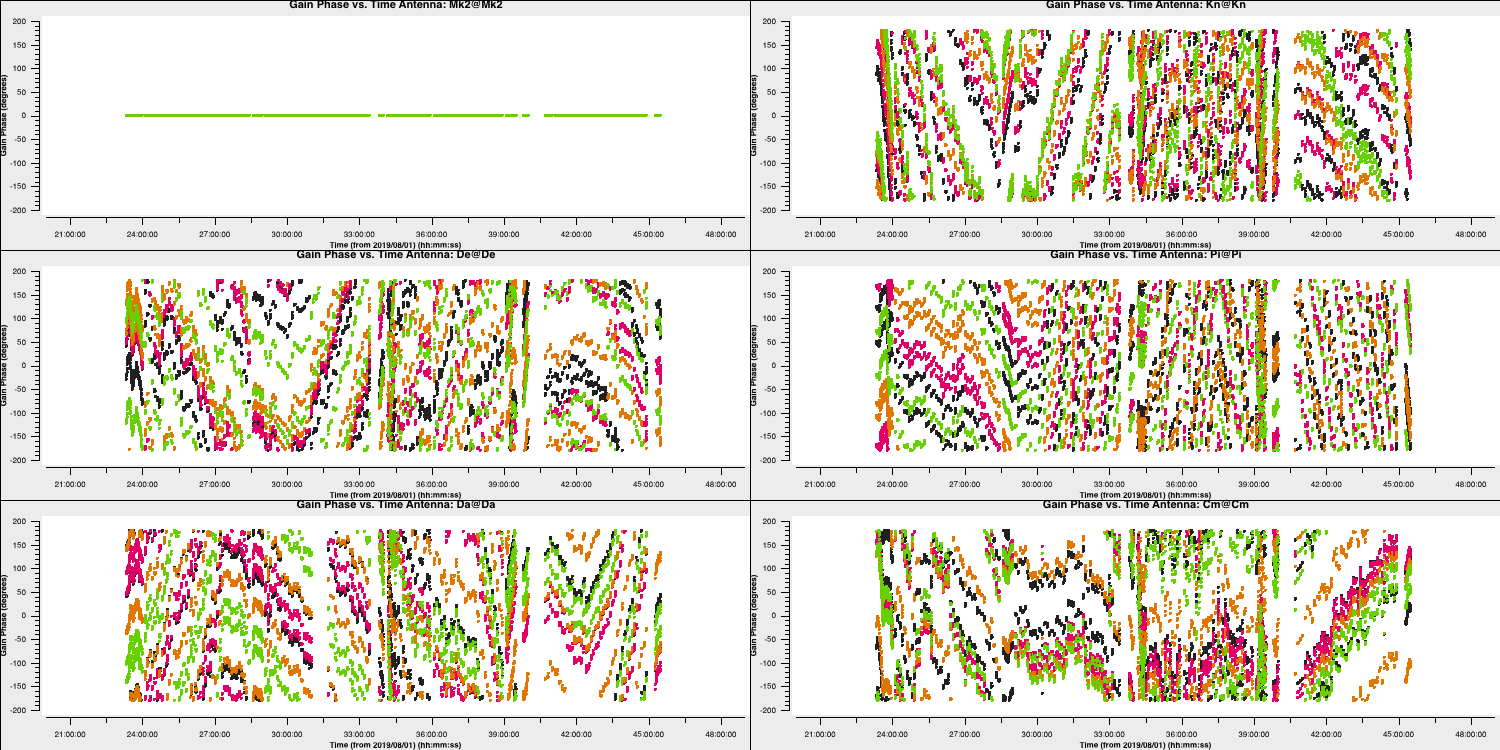
4B. Time dependent amplitude calibration

← back to top

Next we are going to derive time-dependent amplitude solutions for all the calibration sources, applying the delay, bandpass tables and the time-dependent phase solution table.

  • Take a look at the second gaincal entry in step 17 and Iisert a suitable solution interval, the tables to apply and interpolation modes. Note that if you set a solint longer than a single scan on a source, the data will still only be averaged within each scan unless an additional 'combine' parameter is set (not needed here).
    	gaincal(vis='all_avg.ms',
			calmode='a',
			caltable='calsources.a1',
			field='**,**,**',
			solint='**',
			solnorm=False,
			refant=antref,
			minblperant=2,minsnr=2,
			gaintable=['**','**','**'],
			interp=['linear','nearest,nearest','**'])
  • The logger shows a similar proportion of expected:attempted solution intervals as for phase, but those with failed phase solutions are not attempted so all the attempted solutions work. Plot these solutions to ensure they look ok

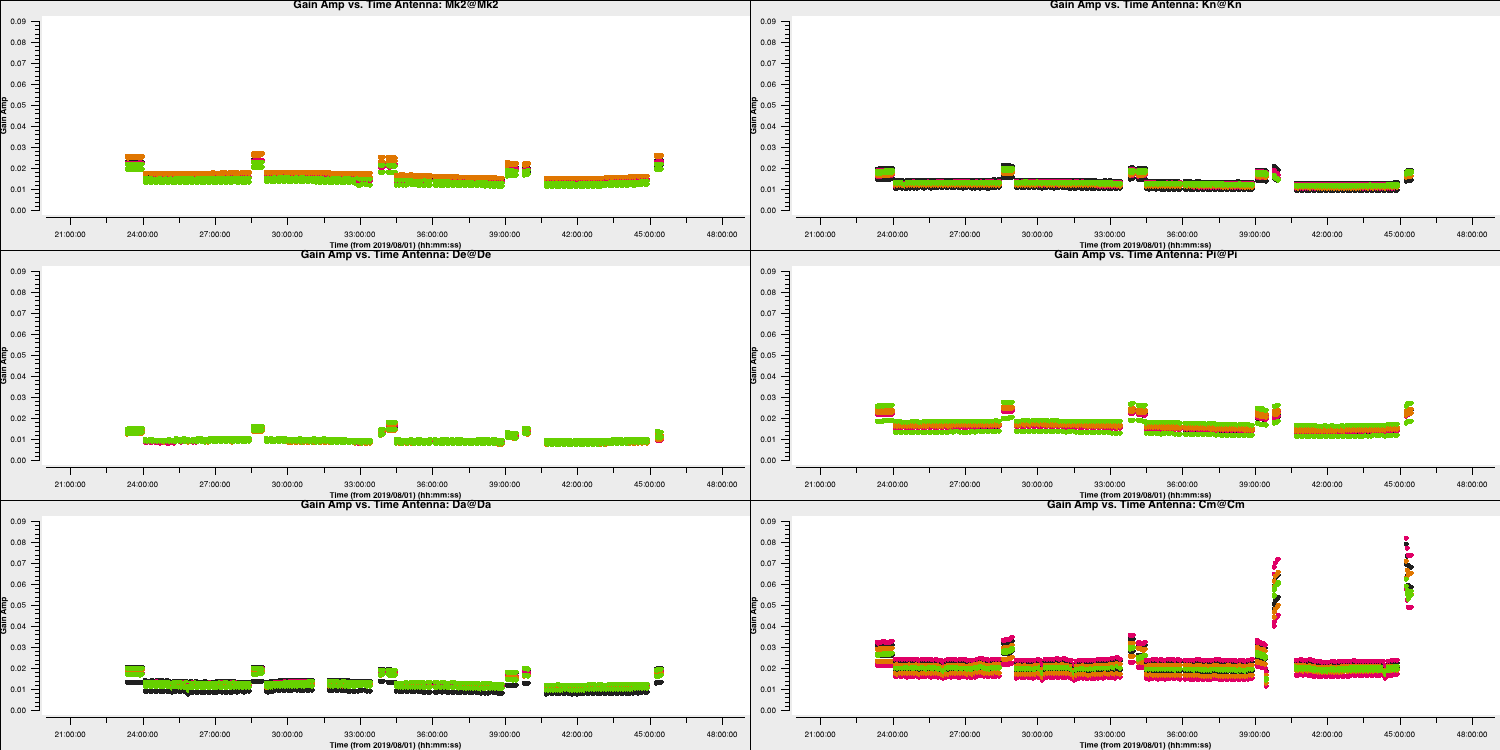
The plot above shows the time dependent amplitude solutions on just the L polarisation and coloured by spw. The solutions for each separate source look similar but there are big differences between sources, since they have all (apart from 1331+3030 and 0319+4130) been compared with a 1 Jy model but they have different flux densities.

5. Determining true flux densities of other calibration sources (steps 18-19)

← back to top

The solutions for 1331+3030 in calsources.a1 contain the correct scaling factor to convert the raw units from the correlator to Jy as well as removing time-dependent errors. This is used to calculate the scaling factor for the other calibration sources in the CASA task fluxscale. We run this task in a different way because the calculated fluxes are returned in the form of a python dictionary. They are also written to a text file. Only the best data are used to derive the flux densities but the output is valid for all antennas. This method assumes that all sources without starting models are points, so it cannot be used for an extended target.

  • We are not going to input anything for step 18 so just run it and we shall look at the outputs

	os.system('rm -rf calsources.a1_flux calsources_flux.txt')
	calfluxes=fluxscale(vis='all_avg.ms',
						caltable='calsources.a1',
						fluxtable='calsources.a1_flux',
						listfile='calsources_flux.txt',
						gainthreshold=0.3,
						antenna='!De',      # Least sensitive
						reference='1331+3030',
						transfer=phref)

If you type calfluxes (once the step has been run) this will show you the python dictionary.

The individual spw estimates may have uncertainties up to $∼20\%$ but the bottom lines give the fitted flux density and spectral index for all spw which should be accurate to a few percent. These require an additional scaling of 0.938 to allow for the resolving out of flux of 1331+3130 by e-MERLIN. The python dictionary calfluxes is edited to do this: 

	eMcalfluxes={}
	for k in calfluxes.keys():
		if len(calfluxes[k]) > 4:
			a=[]
			a.append(calfluxes[k]['fitFluxd']*eMfactor)
			a.append(calfluxes[k]['spidx'][0])
			a.append(calfluxes[k]['fitRefFreq'])
			eMcalfluxes[calfluxes[k]['fieldName']]=a

Next we use setjy in a loop to set each of the calibration source flux densities. The logger will report the values being set.

	for f in eMcalfluxes.keys():
		setjy(vis='all_avg.ms',
			  field=f,
			  standard='manual',
			  fluxdensity=eMcalfluxes[f][0],
			  spix=eMcalfluxes[f][1],
			  reffreq=str(eMcalfluxes[f][2])+'Hz')

The default in setjy is to scale by the spectral index for each channel . Finally we plot the models for the bandpass calibrators, amplitude against frequency, to see the spectral slopes.

	plotms(vis='all_avg.ms', field=phref, xaxis='frequency',
		   yaxis='amp',ydatacolumn='model',
		   coloraxis='spw',correlation='RR',
		   customsymbol=True,symbolshape='circle', symbolsize=5,
		   showgui=gui,overwrite=True,
		   plotfile='phref_model.png')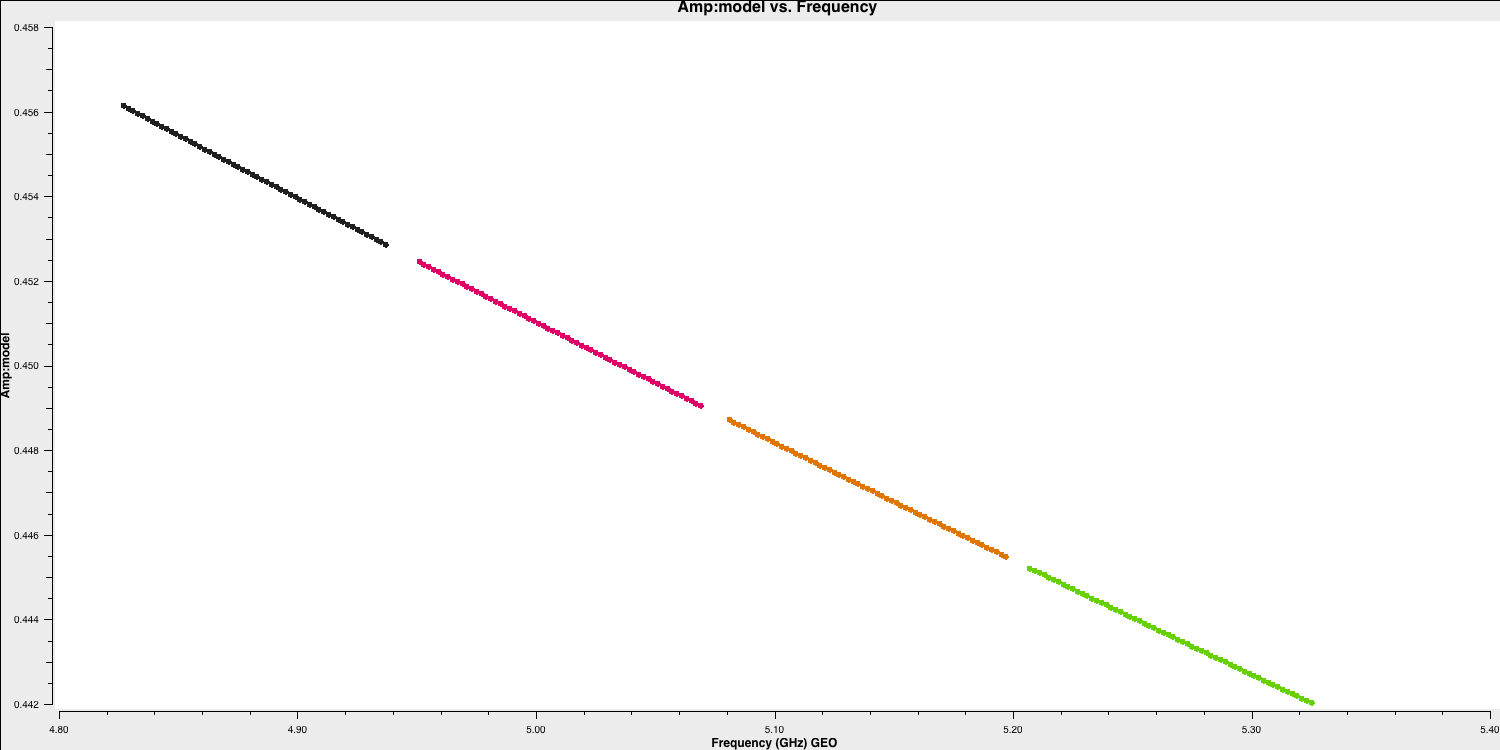

  • Move onto step 19 and look at the inputs and run the step. Again, we won't be inputting parameters here. We are going to now use these new found flux densities to scale our visibilities to the correct, physical values using an amplitude correction.
    	gaincal(vis='all_avg.ms',
			calmode='a',
			caltable='calsources.a2',
			field=calsources,
			solint='inf',
			refant=antref,
			minblperant=2,minsnr=2,
			gaintable=['all_avg.K','bpcal.B1','calsources.p1'],
			interp=['linear','','linear'])

	# Plot solutions
	plotms(vis='calsources.a2',
	       xaxis='time',
	       yaxis='amp',
	       gridrows=3,gridcols=2,
	       iteraxis='antenna', coloraxis='spw',
	       xselfscale=True,
	       yselfscale=True,
	       showgui=gui,overwrite=True,
	       plotfile='calsources.a2.png')

This should produce a plot that that shown below:

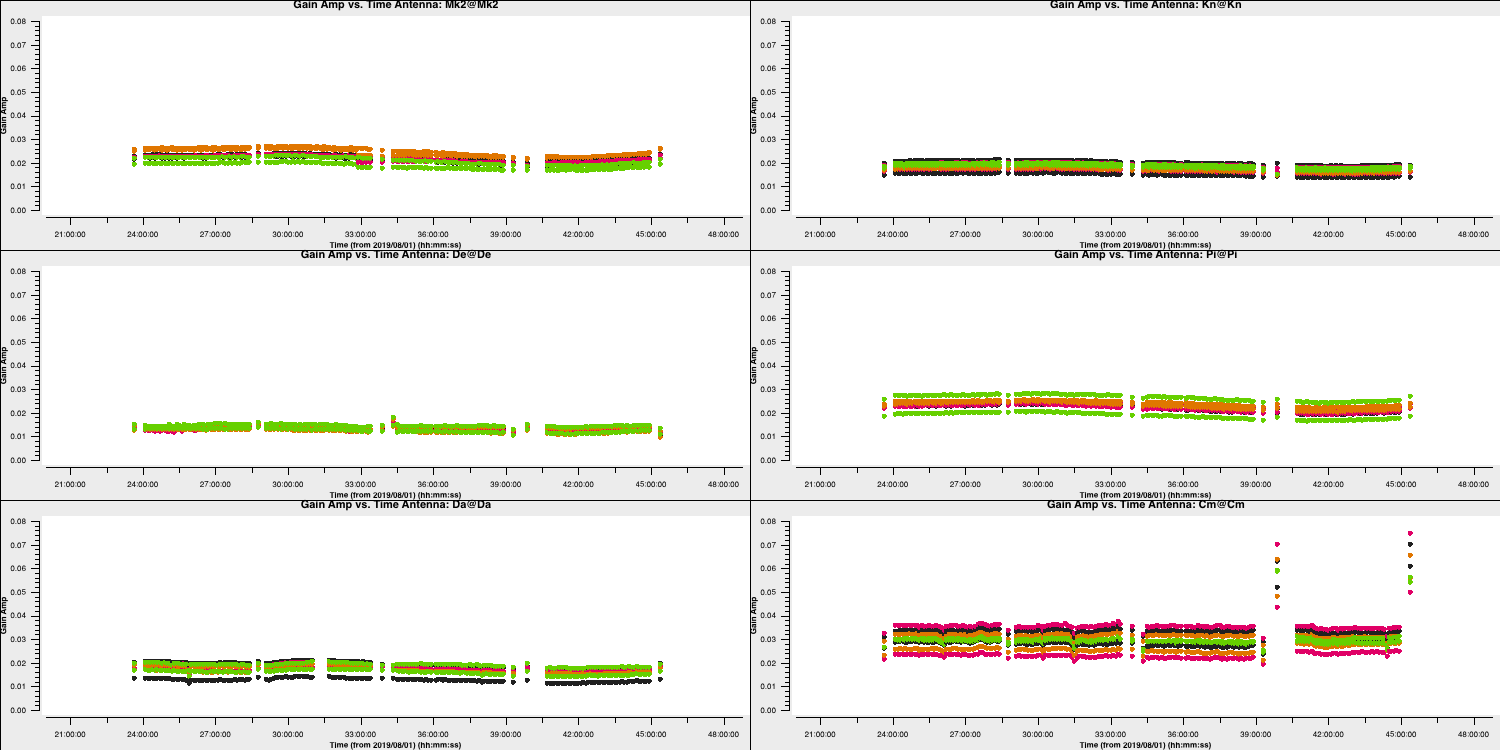
You expect to see a similar scaling factor for all sources. 1331+305 is somewhat resolved, giving slightly higher values for Cm (the antenna giving the longest baselines).

In the final part of the section we are going to derive phase solutions again but now combining all data on the phase calibrator source. This is because we only need one solution to interpolate across the target scans. We derive these and plot them with the following code

	gaincal(vis='all_avg.ms',
			calmode='p',
			caltable='phref.p2',
			field=phref,
			solint='inf',
			refant=antref,
			refantmode='strict',
			minblperant=2,minsnr=2,
			gaintable=['all_avg.K','bpcal.B1'],
			interp=['linear',''])

	# Plot solutions
	plotms(vis='phref.p2',
	       xaxis='time',
	       yaxis='phase',
	       gridrows=3,gridcols=2,
	       iteraxis='antenna', coloraxis='spw',
	       xselfscale=True,
	       yselfscale=True,
	       showgui=gui,overwrite=True,
	       plotfile='phref.p2.png')
	os.system('mv phref.p2?*.png phref.p2.png')

This should produce a plot like that shown below:

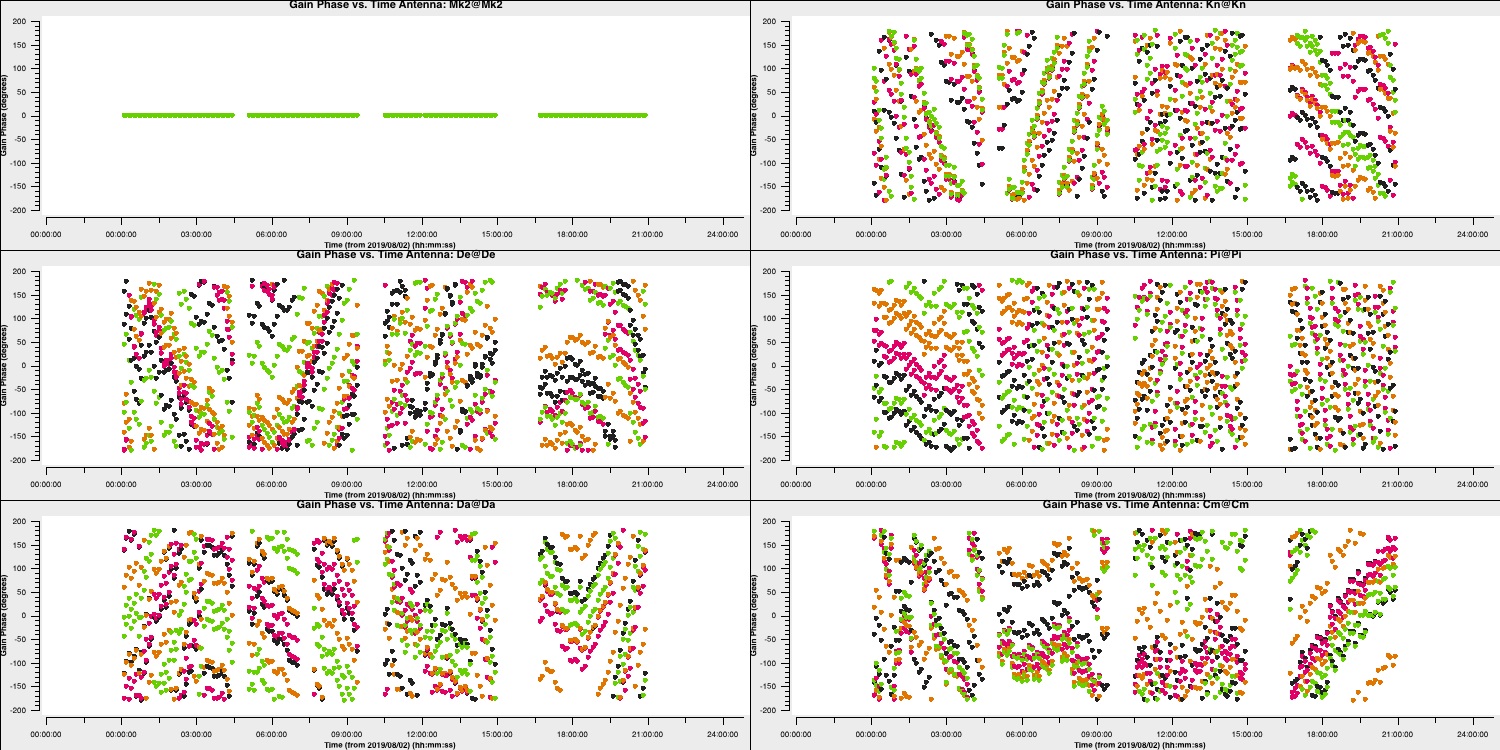
6. Apply solutions to target (steps 20-21)

← back to top

  • Look and execute step 20 while reading the following information about this step.

This step will apply the bandpass correction to all sources. For the other gaintables, for each calibrator (field), the solutions for the same source (gainfield) are applied. gainfield='' for the bandpass table means apply solutions from all fields in that gaintable. applymode='calflag' will flag data with failed solutions which is ok as we know that these were due to bad data. We use a loop over all calibration sources. 

	cals=bases
	cals.remove(target)
	for c in cals:
		applycal(vis='all_avg.ms',
				 field=c,
				 gainfield=[c, '',c,c],
				 calwt=False,
				 applymode='calflag',
				 gaintable=['all_avg.K','bpcal.B1','calsources.p1','calsources.a2'],
				 interp=['linear','nearest','linear','linear'],
				 flagbackup=False)

We then apply the phase-ref solutions to the target. We assume that the phase reference scans bracket the target scans so linear interpolation is used except for bandpass. 

	applycal(vis='all_avg.ms',
			 field='1252+5634',
			 gainfield=['1302+5748','','1302+5748','1302+5748'],
			 calwt=False,
			 applymode='calflag',  # Not too many failed solutions -  OK to flag target data
			 gaintable=['all_avg.K','bpcal.B1','phref.p2','calsources.a2'],
			 interp=['linear','nearest','linear','linear'],
		 	 flagbackup=True)
Next we want to visualise our target and phase reference source. We want to ensure that the phase reference source is a true point source and if there is structure on the target. We can do this by looking at the amp vs uv distance plots. Remember a point source will be flat across uv distance! 

	plotms(vis='all_avg.ms', field='1302+5748', xaxis='uvdist',
		   yaxis='amp',ydatacolumn='corrected',
		   avgchannel='64',correlation='LL,RR',coloraxis='spw',
		   overwrite=True, showgui=gui,
		   plotfile='1302+5748_amp-uvdist.png')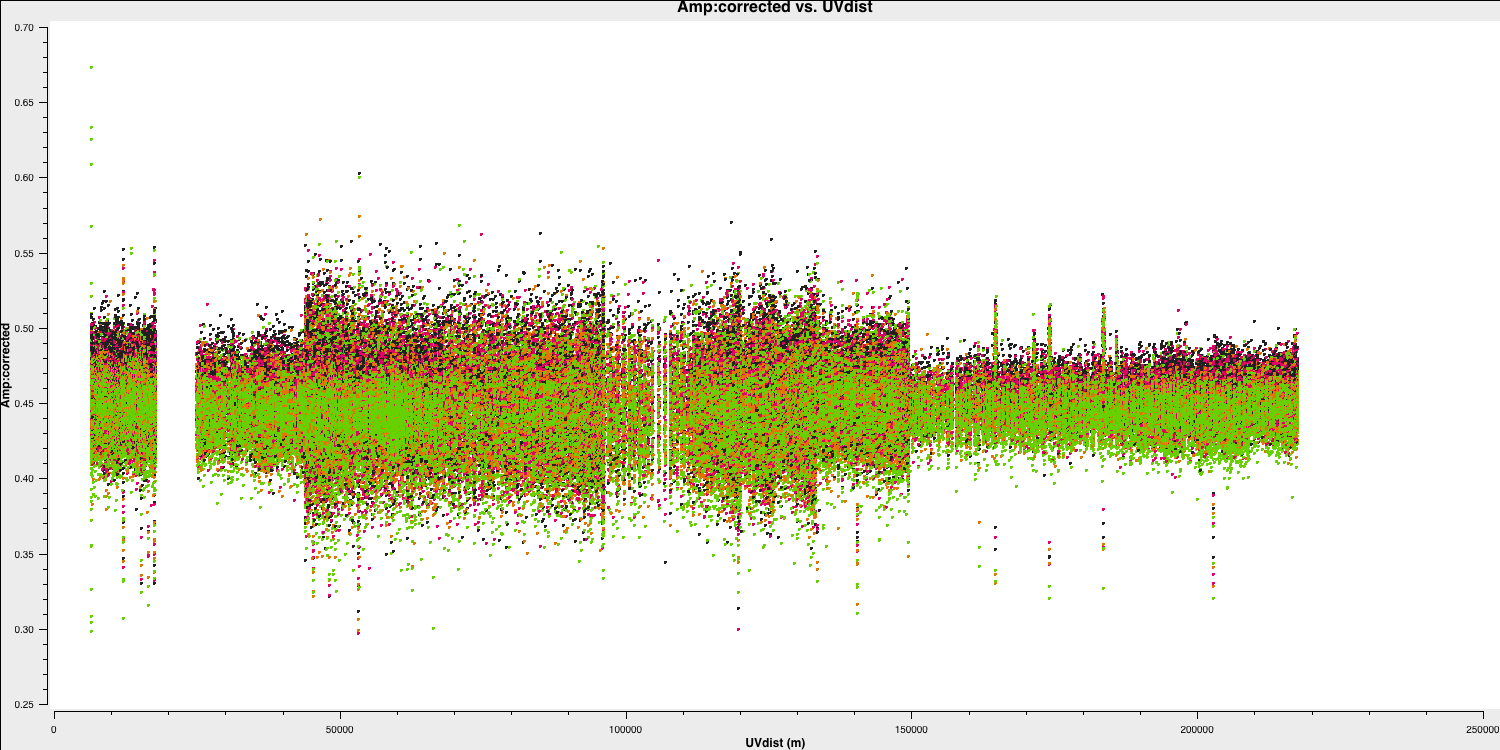

This looks pretty point-like!. Let's repeat the above for the target.

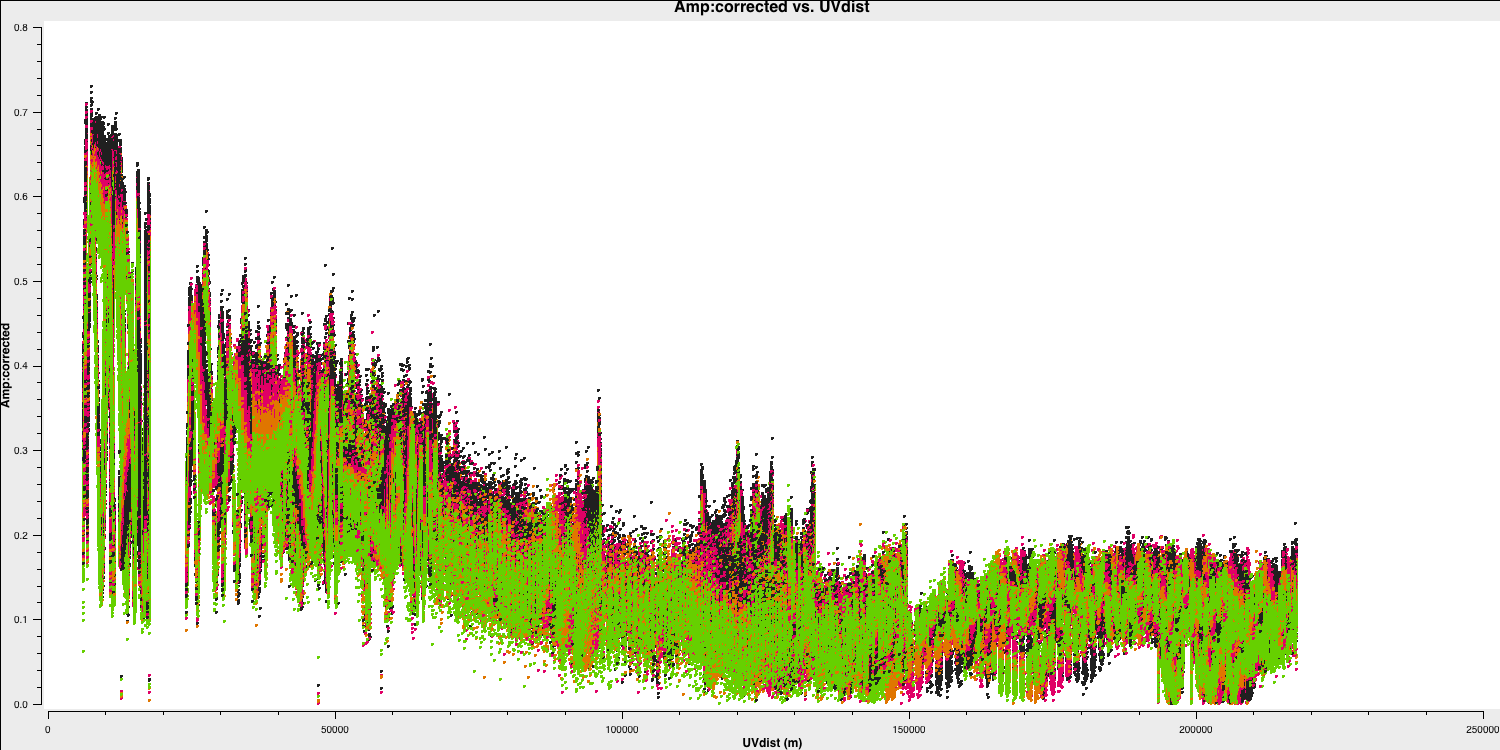
Hurray, there's some structure here!

As a test, QUESTION 5: What do the plots of amplitude against $uv$ distance tell you?

Click for answerThe visibility amplitudes for the phase ref are constant as a function of projected baseline length ($uv$ distance in metres), showing that it is point-like at e-MERLIN resolutions.
The amplitudes are noisiest out to 130km as these are the Defford baselines which are less sensitive. There's a little data which is anomalously low but this is ok as the target is bright.
The target has higher amplitudes on shorter baselines, showing that it has structure on scales larger than 50mas, and has complex structure on the long baselines.

Finally in step 21, we are going to split out the target source. 

	mstransform(vis='all_avg.ms',
										field='1252+5634',
										correlation='LL,RR',
										outputvis='1252+5634.ms',
										keepflags=False,
										usewtspectrum=True,
										timeaverage=True,
										timebin='16s',
										chanaverage=True,
										chanbin=4)

  • Execute step 21.

The task mstranform will make a new measurement set called 1252+5634.ms which contains the calibrated visibilities of the target source (moving the CORRECTED data to the DATA column in the new measurement set). This means we don't need to apply those tables on the fly when we do further calibration. We have also specified some averaging so that the next steps of the tutorial can be processed quicker. In step 21, you will see that another listobs is run for to look at, and we have phase rotated the data to make the imaging steps easier. If you wish to have more information on this, ask your tutor.

This concludes the calibration section. Make sure that you save 1252+5634.ms for the imaging and self-calibration tutorials.

Congratulations, you have finished the second part of this tutorial and calibrated your data. Next we shall move onto imaging your objects. Follow the link below to continue.